题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足a=2sin A, +
+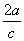 +
+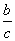 =0.
=0.
(1)求c的值;
(2)求△ABC面积的最大值.
解:(1)∵ +
+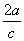 +
+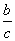 =0,
=0,
∴ccos B+2acos C+bcos C=0,
∴sin Ccos B+sin Bcos C+2sin Acos C=0,
∴sin A+2sin Acos C=0.∵sin A≠0,
 ∴3ab≤3,即ab≤1,当且仅当a=b=1时,取等号,
∴3ab≤3,即ab≤1,当且仅当a=b=1时,取等号,
∴S△ABC=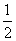 absin C≤
absin C≤ ,∴△ABC面积的最大值为
,∴△ABC面积的最大值为 .
.

练习册系列答案
相关题目
 .
.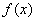 的单调区间与极值;
的单调区间与极值; ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求
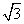 ≈1.73)
≈1.73)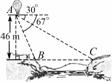 图13
图13 =____________.
=____________.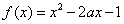 ,当
,当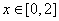 上有最小值
上有最小值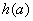 ,最大值为
,最大值为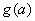
 ,
, 的最小值为
的最小值为 ,求
,求 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围 求这个二次函数的解析式,并写出函数的值域和单调区间?
求这个二次函数的解析式,并写出函数的值域和单调区间? 所表不的区域为
所表不的区域为 ,求区域
,求区域