题目内容
10双互不相同的鞋子混装在一个袋子中,从中任意取4只,4只鞋子中有两只成双,另两只不成双的取法数为_ .
1440
本试题主要是考查了排列组合的运用。
先从10双鞋子中选取一双,有C101种选法,再从9双鞋子中选取2双,有C92种选法,其中从每双鞋子中各取一只分别有2种选法,故共有C101C9222=1440种选法,故答案为1440.
本题也可以这样解:先从10双鞋子中选取一双,有C101种选法,再从9双鞋子中选取2双,有C92种选法,其中从每双鞋子中各取一只分别有2种选法,故共有C101C9222=1440种选法.
先从10双鞋子中选取一双,有C101种选法,再从9双鞋子中选取2双,有C92种选法,其中从每双鞋子中各取一只分别有2种选法,故共有C101C9222=1440种选法,故答案为1440.
本题也可以这样解:先从10双鞋子中选取一双,有C101种选法,再从9双鞋子中选取2双,有C92种选法,其中从每双鞋子中各取一只分别有2种选法,故共有C101C9222=1440种选法.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
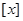 表示不超过
表示不超过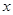 的最大整数(如
的最大整数(如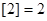 ,
,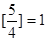 ),对于给定的
),对于给定的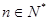 ,定义
,定义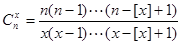 ,
,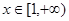 ,则当
,则当 时,函数
时,函数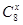 的值域是( )
的值域是( )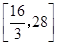
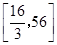
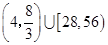
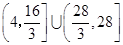
 展开式中
展开式中 的系数是 。
的系数是 。