题目内容
14.关于函数y=sin2x的判断,正确的是( )| A. | 最小正周期为2π,值域为[-1,1],在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上是单调减函数 | |
| B. | 最小正周期为π,值域为[-1,1],在区间[0,$\frac{π}{2}$]上是单调减函数 | |
| C. | 最小正周期为π,值域为[0,1],在区间[0,$\frac{π}{2}$]上是单调增函数 | |
| D. | 最小正周期为2π,值域为[0,1],在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上是单调增函数 |
分析 先化简函数,再利用余弦函数的图象与性质,即可得出结论.
解答 解:y=sin2x=$\frac{1}{2}$(1-os2x)=-$\frac{1}{2}$cos2x+$\frac{1}{2}$
∴函数的最小正周期为π,值域为[0,1],在区间[0,$\frac{π}{2}$]上是单调增函数,
故选C.
点评 本题考查三角函数的化简,考查余弦函数的图象与性质,属于中档题.

练习册系列答案
相关题目
2.已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于点(1,0)对称,则tanφ=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
19.(3-2x-x4)(2x-1)6的展开式中,含x3项的系数为( )
| A. | 600 | B. | 360 | C. | -600 | D. | -360 |
1.已知函数f(x)=aex-x2-(3a+1)x,若函数f(x)在区间(0,ln3)上有极值,则实数a的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-1) | C. | (-1,-$\frac{1}{2}$) | D. | (-∞,-2)∪(0,1) |
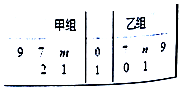 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.