题目内容
正四面体A-BCD中E、F分别是棱BC和AD之中点，则EF和AB所成的角（ ）
分析：取AC的中点H，连接FH、EH、FC、FB．设正四面体棱长为2a，可以求得BF=CF=
a，所以在等腰△BCF中，求出EF=
a．在△ABC中，利用中位线得EH∥AB，所以∠FEH或其补角就是EF和AB所成的角．最后在△EFH中，根据HE=HF=a，EF=
a，利用余弦定理，可得cos∠FEH=
，所以∠FEH=45°，从而得到正确答案．
| 3 |
| 2 |
| 2 |
| ||
| 2 |
解答：解：取AC的中点H，连接FH、EH、FC、FB
设正四面体棱长为2a，则
等边△ABD中，中线BF=
•2a=
a，同理可得CF=
a，
∴△FBC中，BF=CF=
a，BC=2a，E是BC中点
所以，由勾股定理得EF=
=
a
∵△ABC中，E、H分别是BC、AC的中点
∴EH∥AB，可得∠FEH或其补角就是EF和AB所成的角
∵HE、HF分别是等边△ABC、等边△ADC的中位线
∴HE=HF=a
∵△EFH中，HE=HF=a，EF=
a
∴cos∠FEH=
=
，可得∠FEH=45°
即异面直线EF和AB所成的角为45°．
故选A
设正四面体棱长为2a，则
等边△ABD中，中线BF=
| ||
| 2 |
| 3 |
| 3 |
∴△FBC中，BF=CF=
| 3 |
所以，由勾股定理得EF=
| BF2-BE2 |
| 2 |
∵△ABC中，E、H分别是BC、AC的中点
∴EH∥AB，可得∠FEH或其补角就是EF和AB所成的角
∵HE、HF分别是等边△ABC、等边△ADC的中位线
∴HE=HF=a
∵△EFH中，HE=HF=a，EF=
| 2 |
∴cos∠FEH=
| EH2+EF2-FH2 |
| 2•EH•EF |
| ||
| 2 |
即异面直线EF和AB所成的角为45°．
故选A
点评：本题给出正四面体一组对棱的中点，求它们的连线与异面的棱所成的角，着重考查了空间异面直线及其所成的角的求法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
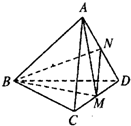8、棱长都相等的四面体称为正四面体．在正四面体A-BCD中，点M，N分别是CD和AD的中点，
如图，在棱长为2的正四面体A-BCD中，若以△ABC为视角正面，则其正视图的面积是（ ）
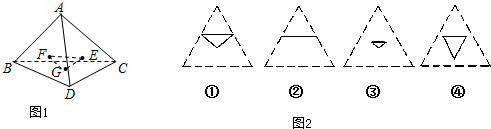
设正四面体A-BCD中，E、F分别为AC、AD的中点，则△BEF在该四面体的面ADC上的射影可能是（ ）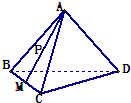
在正四面体A-BCD中，棱长为4，M是BC的中点，P在线段AM上运动（P不与A、M重合），过点P作直线l⊥平面ABC，l与平面BCD交于点Q，给出下列命题：①BC⊥面AMD；②Q点一定在直线DM上 ③VC-AMD=4