题目内容
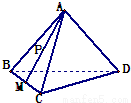
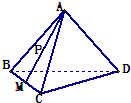 在正四面体A-BCD中,棱长为4,M是BC的中点,P在线段AM上运动(P不与A、M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥面AMD;②Q点一定在直线DM上 ③VC-AMD=4
在正四面体A-BCD中,棱长为4,M是BC的中点,P在线段AM上运动(P不与A、M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥面AMD;②Q点一定在直线DM上 ③VC-AMD=4| 2 |
| A、①② | B、①③ | C、②③ | D、①②③ |
分析:①因为AM⊥BC,DM⊥BC所以BC⊥平面ADM.故①正确
②因为PQ⊥平面BCD,BC?平面BCD所以PQ⊥BC因为P∈AM所以P∈平面AMD因为BC⊥平面AMD所以Q∈平面AMD因为平面AMD∩平面BCD=MD所以Q∈MD故②正确.
③因为BC⊥平面ADM∴把MC作为四面体C-MAD的高,△AMD为其底面,S△AMD=4
,VC-AMD=
.故③错误
②因为PQ⊥平面BCD,BC?平面BCD所以PQ⊥BC因为P∈AM所以P∈平面AMD因为BC⊥平面AMD所以Q∈平面AMD因为平面AMD∩平面BCD=MD所以Q∈MD故②正确.
③因为BC⊥平面ADM∴把MC作为四面体C-MAD的高,△AMD为其底面,S△AMD=4
| 2 |
8
| ||
| 3 |
解答:解:∵A-BCD为正四面体且M为BC的中点
∴AM⊥BC,DM⊥BC
又∵AM∩DM=M
∴BC⊥平面ADM
故①正确.
∵PQ⊥平面BCD,BC?平面BCD
∴PQ⊥BC
又∵P∈AM∴P∈平面AMD
又∵BC⊥平面AMD
∴Q∈平面AMD
又∵平面AMD∩平面BCD=MD
∴Q∈MD
故②正确.
由①得BC⊥平面ADM∴把MC作为四面体C-MAD的高,△AMD为其底面
在三角形△AMD中AM=MD=2
,AD=4
∴S△AMD=4
∴VC-AMD=
×4
×2=
故③错误.
故选A.
∴AM⊥BC,DM⊥BC
又∵AM∩DM=M
∴BC⊥平面ADM
故①正确.
∵PQ⊥平面BCD,BC?平面BCD
∴PQ⊥BC
又∵P∈AM∴P∈平面AMD
又∵BC⊥平面AMD
∴Q∈平面AMD
又∵平面AMD∩平面BCD=MD
∴Q∈MD
故②正确.
由①得BC⊥平面ADM∴把MC作为四面体C-MAD的高,△AMD为其底面
在三角形△AMD中AM=MD=2
| 3 |
∴S△AMD=4
| 2 |
∴VC-AMD=
| 1 |
| 3 |
| 2 |
8
| ||
| 3 |
故③错误.
故选A.
点评:证明线面垂直要找到直线与平面内的两条相交直线都垂直这是关键;证明点在直线上只要证明点在两个平面的交线上即可;求四面体的体积关键是找到合适的底面与高即底面与高要简单易求.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
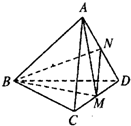 8、棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,
8、棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,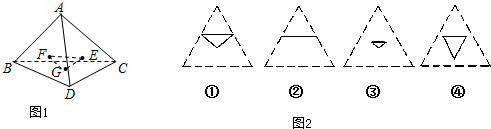
 .其中正确的是( )
.其中正确的是( )