Question

已知点P（0，5）及圆C：x²+y²+4x-12y+24=0.

（1）若直线l过P且被圆C截得的线段长为4，求l的方程；

（2）求过P点的圆C的弦的中点的轨迹方程.

Answer 1

（1）3x-4y+20=0或x=0（2）x²+y²+2x-11y+30=0.        

解析:

（1）方法一  如图所示，AB=4，D是AB的中点，CD⊥AB，AD=2，圆x²+y²+4x-12y+24=0可化为（x+2）²+（y-6）²=16，圆心C（-2，6），半径r=4，故AC=4，

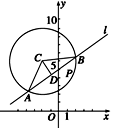
在Rt△ACD中，可得CD=2.                                                                                     2分

设所求直线的斜率为k，则直线的方程为y-5=kx,

即kx-y+5=0.

由点C到直线AB的距离公式： =2，得k=.

此时直线l的方程为3x-4y+20=0.                                                                            4分

又直线l的斜率不存在时，此时方程为x=0.                                                               6分

则y²-12y+24=0,∴y₁=6+2,y₂=6-2,

∴y₂-y₁=4,故x=0满足题意.

∴所求直线的方程为3x-4y+20=0或x=0.                                                                               8分

方法二 设所求直线的斜率为k，则直线的方程为

y-5=kx,即y=kx+5,

联立直线与圆的方程

消去y得（1+k²）x²+(4-2k)x-11=0                                                                                    ①     2分

设方程①的两根为x₁,x₂,

由根与系数的关系得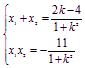                                                                      ②  4分

由弦长公式得|x₁-x₂|=

将②式代入，解得k=，

此时直线的方程为3x-4y+20=0.                                                                                        6分

又k不存在时也满足题意，此时直线方程为x=0.

∴所求直线的方程为x=0或3x-4y+20=0.                                                                               8分

（2）设过P点的圆C的弦的中点为D（x,y）,

则CD⊥PD，即·=0，                                                                                           10分

（x+2,y-6）·(x,y-5)=0,化简得所求轨迹方程为

x²+y²+2x-11y+30=0.                                                                                                                         12分