题目内容
江岸边有一炮台高30米，江中有两条船，由炮台顶部测得俯角分别为45°和30°，而且两条船与炮台底部连线成30°角，则两条船相距（ ）
分析：利用直线与平面所以及俯角的定义，化为两个特殊直角三角形的计算，再在底面△BCD中用余弦定理即可求出两船距离．
解答：解：如图，过炮台顶部A作水平面的垂线，垂足为B，设A处观测小船C的俯角为45°，
设A处观测小船D的俯角为30°，连接BC、BD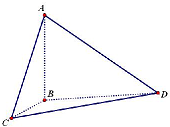
Rt△ABC中，∠ACB=45°，可得BC=AB=30米
Rt△ABD中，∠ADB=30°，可得BD=
AB=30
米
在△BCD中，BC=30米，BD=30
米，∠CBD=30°，
由余弦定理可得：
CD2=BC2+BD2-2BC•BDcos30°=900
∴CD=30米（负值舍去）
故选：C
设A处观测小船D的俯角为30°，连接BC、BD
Rt△ABC中，∠ACB=45°，可得BC=AB=30米
Rt△ABD中，∠ADB=30°，可得BD=
| 3 |
| 3 |
在△BCD中，BC=30米，BD=30
| 3 |
由余弦定理可得：
CD2=BC2+BD2-2BC•BDcos30°=900
∴CD=30米（负值舍去）
故选：C
点评：本题给出实际应用问题，求炮台旁边两条小船距的距离．着重考查了余弦定理、空间线面的位置关系等知识，属于中档题．熟练掌握直线与平面所成角的定义与余弦定理解三角形，是解决本题的关键．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
，而且两条船与炮台底部连线成
角，那么这两条船相距多少米.