题目内容
设数列{ }的前n项和为
}的前n项和为 ,且方程
,且方程 有一根
有一根
为 ,
, 
(1) 求 ,
, ;
;
(2) 猜想数列{ }的通项公式,并给出严格的证明.
}的通项公式,并给出严格的证明.
解:(1)当n=1时, 有一根为
有一根为 =
= -1,
-1,
于是( -1)2-
-1)2- (
( -1)-
-1)- =0,解得
=0,解得 =1/2.
=1/2.
当n=2时, 有一根为
有一根为 =
= ,
,
于是( -1/2)2-
-1/2)2- (
( -1/2)-
-1/2)- =0,解得
=0,解得 =1/6 .
=1/6 .
(2)由题设( -1)2-
-1)2- (
( -1)-
-1)- =0,
=0,
 -2
-2 +1-
+1-
 =0 当n≥2时,
=0 当n≥2时, =
= -
- ,
,
代入上式得 -2
-2 +1=0.①.
+1=0.①.
由(1)得S1= =1/2,
=1/2, =
= +
+ =1/2+1/6=2/3.
=1/2+1/6=2/3.
由①可得s3=3/4.由此猜想 =n/n+1,n=1,2,3,
=n/n+1,n=1,2,3,
下面用数学归纳法证明这个结论.(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即 =k/k+1,当n=k+1时,由①得
=k/k+1,当n=k+1时,由①得 =12-Sk,
=12-Sk,
即 =k+1/k+2,故n=k+1时结论也成立
=k+1/k+2,故n=k+1时结论也成立
综上,由(i)、(ii)可知 =n/n+1对所有正整数n都成立..
=n/n+1对所有正整数n都成立..

练习册系列答案
相关题目
 。
。 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 sinB-2sinA=0,
sinB-2sinA=0, 。
。
 B.
B. C.
C. D.
D.

 ,分布列为
,分布列为

 的值;
的值;  ,
, 与方差
与方差 ;并分析甲,乙的技术状况。
;并分析甲,乙的技术状况。  )
)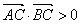 ; 条件乙:点C的坐标是方程
; 条件乙:点C的坐标是方程 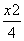 +
+ 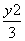 = 1 (y¹0)的解. 则甲是乙的( )
= 1 (y¹0)的解. 则甲是乙的( )  :
: ,
, :
: ,若
,若 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是 .
的取值范围是 .  +2x+m (m为常数),则
+2x+m (m为常数),则 ( )
( ) D.
D.
 的导数为
的导数为 ,
, ,对于任意实数
,对于任意实数 ,有
,有 ,则
,则 的最小值为 ( )
的最小值为 ( ) B.
B. C.
C. D.
D.