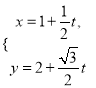题目内容

【题目】选修4－4：坐标系与参数方程

已知在平面直角坐标系中，曲线的参数方程是 (为参数)，以坐标原点为极点， 轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程是．

(Ⅰ) 求曲线与交点的平面直角坐标；

(Ⅱ) 点分别在曲线， 上，当最大时，求的面积(为坐标原点)．

【答案】（Ⅰ）.（Ⅱ）

【解析】试题分析：

(1)分别求得两圆的标准方程，然后联立两方程即可求得

(2)利用几何性质首先确定三角形面积最大时 的方程,然后结合点到直线的距离公式求解三角形的高，据此即可求得三角形面积的最大值.

试题解析：

(Ⅰ)由得

则曲线的普通方程为.

又由，得，得.

把两式作差得， ，代入，

可得交点坐标为为.

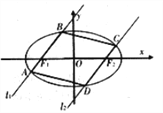
(Ⅱ) 由平面几何知识可知，

当依次排列且共线时， 最大，此时，

直线的方程为，则到的距离为，

所以的面积为.

练习册系列答案
相关题目

【题目】定义：在等式 中，把， ， ，…， 叫做三项式的次系数列(如三项式的1次系数列是1，1，1).

(1)填空：三项式的2次系数列是_______________；

三项式的3次系数列是_______________；

(2)由杨辉三角数阵表可以得到二项式系数的性质,类似的请用三项式次系数列中的系数表示 (无须证明)；

(3)求的值.

【题目】在平面直角坐标系xOy中，椭圆C的参数方程为（θ为参数），直线l的参数方程为（t为参数）．

（Ⅰ）写出椭圆C的普通方程和直线l的倾斜角；

（Ⅱ）若点P（1，2），设直线l与椭圆C相交于A，B两点，求|PA|·|PB|的值．

【题目】如图，四棱锥中，已知平面面， ， ， ， .

（1）求证：平面平面；

（2）直线与平面所成角为，求二面角的平面角的正切值.

【题目】如图，在平面直角坐标系中，椭圆： 的离心率为，直线l：y＝2上的点和椭圆上的点的距离的最小值为1．

(Ⅰ) 求椭圆的方程；

(Ⅱ) 已知椭圆的上顶点为A，点B，C是上的不同于A的两点，且点B，C关于原点对称，直线AB，AC分别交直线l于点E，F．记直线与的斜率分别为， ．

① 求证： 为定值；

② 求△CEF的面积的最小值.

【题目】已知函数的部分图象如图所示.

（1） 求函数的解析式；

（2） 如何由函数的通过适当图象的变换得到函数的图象， 写出变换过程;

（3） 若，求的值.

【题目】设函数f（x）＝|x－1|＋|2x－1|．

（Ⅰ）若对x＞0，不等式f（x）≥tx恒成立，求实数t的最大值M；

（Ⅱ）在（Ⅰ）成立的条件下，正实数a，b满足a2＋b2＝2M．证明：a＋b≥2ab．

【题目】如图，过椭圆： 的左右焦点分别作直线， 交椭圆于与，且.

（1）求证：当直线的斜率与直线的斜率都存在时， 为定值；

（2）求四边形面积的最大值.

【题目】已知函数f（x）=loga（1﹣x）+loga（x+3），其中0＜a＜1．
（1）求函数f（x）的定义域；
（2）若函数f（x）的最小值为﹣4，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网