题目内容
已知O是△ABC内任意一点,连结AO、BO、CO并延长交对边于A′,B′,C′,则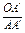 +
+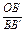 +
+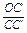 =1,这是一道平面几何题,其证明常采用“面积法”.
=1,这是一道平面几何题,其证明常采用“面积法”.
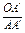 +
+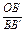 +
+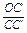 =
=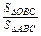 +
+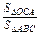 +
+ =
=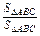 =1,
=1,
请运用类比思想,对于空间中的四面体V—BCD,存在什么类似的结论?并用体积法证明.
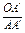 +
+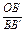 +
+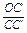 =1,这是一道平面几何题,其证明常采用“面积法”.
=1,这是一道平面几何题,其证明常采用“面积法”.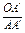 +
+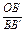 +
+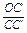 =
=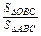 +
+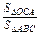 +
+ =
=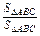 =1,
=1,请运用类比思想,对于空间中的四面体V—BCD,存在什么类似的结论?并用体积法证明.
在四面体O—BCD与V—BCD中: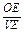 =
=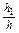 =
=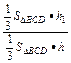 =
= .
.
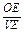 =
=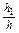 =
=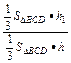 =
= .
.在四面体V—BCD中,任取一点O,连结VO、DO、BO、CO并延长分别交四个面于E、F、G、H点.
则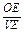 +
+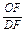 +
+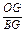 +
+ =1.
=1.
在四面体O—BCD与V—BCD中: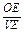 =
=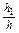 =
=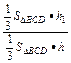 =
= .
.
同理有: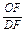 =
=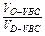 ;
;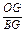 =
=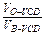 ;
; =
=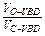 ,
,
∴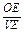 +
+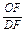 +
+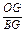 +
+
=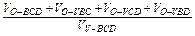 =
=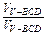 ="1."
="1."
则
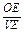 +
+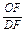 +
+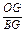 +
+ =1.
=1.在四面体O—BCD与V—BCD中:
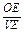 =
=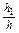 =
=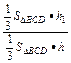 =
= .
.同理有:
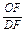 =
=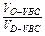 ;
;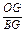 =
=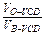 ;
; =
=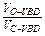 ,
,∴
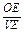 +
+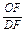 +
+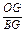 +
+
=
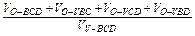 =
=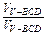 ="1."
="1." 
练习册系列答案
相关题目
 ,
, (其中
(其中 ,且
,且 ).
). 请你推测
请你推测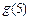 能否用
能否用 来表示;
来表示; ,请依据:
,请依据: ;
; ;
; ;归纳出
;归纳出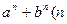 为正整数)满足的不等式,并予以证明;
为正整数)满足的不等式,并予以证明; -i为纯虚数,则实数a= 。
-i为纯虚数,则实数a= 。 ; ⑵
; ⑵ ,归纳其特点可以获得一个猜想是:
,归纳其特点可以获得一个猜想是: .
.