题目内容
过双曲线的一焦点的直线垂直于一渐近线,且与双曲线的两支相交,求该双曲线离心率的范围。
![]()
解析:
设双曲线的方程为![]() ,
,![]() ,渐近线
,渐近线![]() ,则过
,则过![]() 的直线方程为
的直线方程为![]() ,则
,则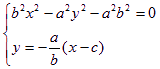 ,
,
代入得![]() ,
,
∴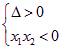 即得
即得![]() ,
,
∴![]() ,即得到
,即得到![]() 。
。
点评:直线与圆锥曲线的位置关系经常和圆锥曲线的几何要素建立起对应关系,取值范围往往与判别式的取值建立联系![]()

练习册系列答案
相关题目
题目内容
过双曲线的一焦点的直线垂直于一渐近线,且与双曲线的两支相交,求该双曲线离心率的范围。
![]()
设双曲线的方程为![]() ,
,![]() ,渐近线
,渐近线![]() ,则过
,则过![]() 的直线方程为
的直线方程为![]() ,则
,则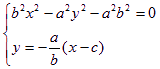 ,
,
代入得![]() ,
,
∴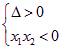 即得
即得![]() ,
,
∴![]() ,即得到
,即得到![]() 。
。
点评:直线与圆锥曲线的位置关系经常和圆锥曲线的几何要素建立起对应关系,取值范围往往与判别式的取值建立联系![]()
