题目内容
(2006
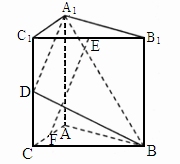
北京海淀模拟)如下图,直三棱柱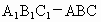 中,
中,
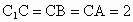
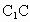 、
、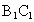 的中点.
的中点.
(1)
求点B到平面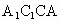 的距离;
的距离;
(2)
求二面角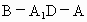 的大小;
的大小;
(3)
在线段AC上是否存在一点F,使得EF上平面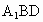 ?若存在,确定其位置并证明结论;若不存在,说明理由.
?若存在,确定其位置并证明结论;若不存在,说明理由.
答案:略
解析:
解析:
|
解析: (1)∵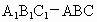 为直三棱柱, 为直三棱柱,
∴ 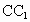 ⊥底面ABC,∴ ⊥底面ABC,∴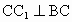 . .
∵ AC⊥CB,∴BC⊥平面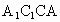 . .
∴ BC长度即为B点到平面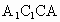 的距离. 的距离.
∵ BC=2,∴点B到平面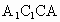 的距离为2. 的距离为2.
(2) 分别延长AC,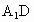 交于G. 交于G.
过 C作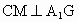 于M,连结BM. 于M,连结BM.
∵ BC⊥平面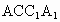 ,∴CM为BM在平面 ,∴CM为BM在平面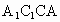 内的射影. 内的射影.
∴ 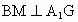 ,∴∠CMB为二面角 ,∴∠CMB为二面角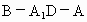 的平面角. 的平面角.
在平面 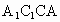 中, 中,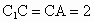 ,D为 ,D为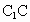 的中点,∴CG=2,DC=1. 的中点,∴CG=2,DC=1.
在直角三角形 CDG中,∴ 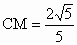 ,∴ ,∴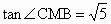 , ,
即二面角 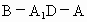 的大小为 的大小为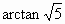 . .
(3) 在线段AC上存在一点F,使得EF⊥平面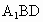
其位置为 AC中点,证明如下:∵ 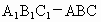 为直三棱柱,∴ 为直三棱柱,∴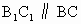 . .
∵由 (1)BC⊥平面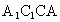 , ,
∴ 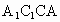 . .
∵ EF在平面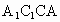 内的射影为 内的射影为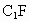 , ,
∵ F为AC中点,∴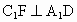 .∴ .∴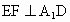 . .
同理可证 EF⊥BD,∴EF⊥平面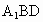 . .
∵ E为定点,平面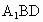 为定平面, 为定平面,
∴点 F唯一. |

练习册系列答案
相关题目
(2006
北京海淀模拟)若直线l∶ax+by=1与圆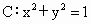 有两个不同交点,则点P(a,b)与圆C的位置关系是
有两个不同交点,则点P(a,b)与圆C的位置关系是
[
]|
A .点在圆上 |
B .点在圆内 |
|
C .点在圆外 |
D .不能确定 |
 平面
平面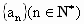 ,满足
,满足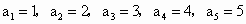 .当n≥5时,
.当n≥5时,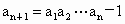 .若数列
.若数列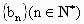 满足
满足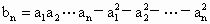 .
.
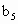 ;
;
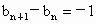 ;
;
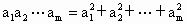 .
.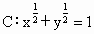 ,给出下列四个命题
,给出下列四个命题
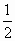 ;
;
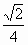 ;
;
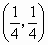 中心对称;
中心对称;
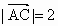 ,
,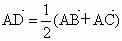 .
.
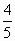 ,且直线l与点D的轨迹相切,求该椭圆的方程.
,且直线l与点D的轨迹相切,求该椭圆的方程.