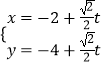题目内容
【题目】设函数f（x）=sinxcosx﹣sin2（x﹣ 
）． （Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求函数f（x﹣ 
）在[0， 
]上的最大值与最小值．
【答案】解：（Ⅰ）∵f（x）=sinxcosx﹣sin2（x﹣ 
）=sin2x﹣ 
， ∴函数f（x）的最小正周期T=π；
（Ⅱ）由（1）得f（x﹣ 
）=sin（2x﹣ 
）﹣ ，
∵x∈[0， 
]，
∴﹣ ≤2x﹣ ≤ 
，
∴sin（2x﹣ ）∈[﹣ 
，1]，
∴f（x﹣ ）∈[﹣ 
， ]，
∴f（x﹣ ）在[0， ]上的最大值是 ，
最小值是﹣ ．
【解析】（Ⅰ）由三角恒等变换化简f（x），得到最小正周期．（Ⅱ）得到f（x﹣ 
）后可以由x的范围得到f（x﹣ ）的值域，由此得到最大最小值．
练习册系列答案
相关题目
