题目内容
【题目】设函数![]()
(1)若![]() 是函数
是函数![]() 的一个极值点,求函数
的一个极值点,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,对于任意的
时,对于任意的![]() (
(![]() 为自然对数的底数)都有
为自然对数的底数)都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)先对函数求导,然后结合极值存在条件可求![]() ,
,![]() 关系,代入后即可求解单调区间;
关系,代入后即可求解单调区间;
(2)先分离出![]() ,转化为求解相应函数的最值或范围,结合导数可求.
,转化为求解相应函数的最值或范围,结合导数可求.
解:(1)定义域![]() ,
,![]() ,
,
由题意可得,![]() (1)
(1)![]() 即
即![]() ,
,
所以![]() ,
,
由函数存在极值可知,![]() ,
,
![]() 时,由
时,由![]() 可得
可得![]() ,函数
,函数![]() 在
在![]() 单调递增,由
单调递增,由![]() 可得
可得![]() ,函数
,函数![]() 在
在![]() 上单调递减.
上单调递减.
![]() 时,由
时,由![]() 可得,
可得,![]() ,函数在
,函数在![]()
![]() 上单调递减,由
上单调递减,由![]() 可得,
可得,![]()
![]() 在
在![]() 单调递增;
单调递增;
![]() 当
当![]() 时,由
时,由![]() 可得,
可得,![]() 或
或![]() ,由
,由![]() 可得,
可得,![]() ,
,
故函数的单调递增区间![]() ,
,![]() 0,
0,![]() ),单调递减区间
),单调递减区间![]() ;
;
综上所述:当![]() ,
,![]() 恒成立,不符合题意;
恒成立,不符合题意;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
(2)![]() 时,
时,![]() 可得,
可得,![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,
,![]()
![]()
则![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() (1)
(1)![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,![]()
![]()
![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() (e)
(e)![]() ,
,
故![]() .
.
故![]() 的范围
的范围![]() ,
,![]() .
.

【题目】随着5G商用进程的不断加快,手机厂商之间围绕5G用户的争夺越来越激烈,5G手机也频频降低身价飞人寻常百姓家.某科技公司为了给自己新推出的5G手机定价,随机抽取了100人进行调查,对其在下一次更换5G手机时,能接受的价格(单位:元)进行了统计,得到结果如下表,已知这100个人能接受的价格都在![]() 之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
分组 | 一 | 二 | 三 | 四 | 五 |
手机价格X(元) |
|
|
|
|
|
频数 | 10 | x | y | 20 | 20 |
(1)现用分层抽样的方法从第一、二、三组中随机抽取6人,将该样本看成一个总体,从中随机抽取2人,求其中恰有1人能接受的价格不低于2000元的概率;
(2)若人们对5G手机能接受的价格X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数
为样本平均数![]() ,
,![]() 为样本方差
为样本方差![]() ,求
,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
【题目】某公司生产一种产品,从流水线上随机抽取100件产品,统计其质量指数并绘制频率分布直方图(如图1):
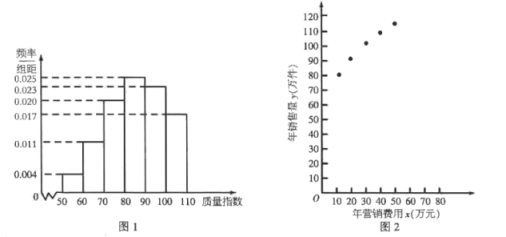
产品的质量指数在![]() 的为三等品,在
的为三等品,在![]() 的为二等品,在
的为二等品,在![]() 的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年的年营销费用
(单位:万件)的影响,对近5年的年营销费用![]() 和年销售量
和年销售量![]()
![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
16.30 | 24.87 | 0.41 | 1.64 |
表中![]() ,
,![]() ,
,![]() ,
,![]()
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
(ⅰ)建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?(收益=销售利润-营销费用,取![]() )
)
参考公式:对于一组数据:![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小乘估计分别为
的斜率和截距的最小乘估计分别为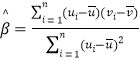 ,
,![]()