题目内容
已知椭圆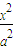
+
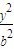=1，（a＞b＞0）的长轴为AB，以AB为底边作椭圆的内接等腰梯形ABCD，求此等腰梯形面积的最大值．
【答案】分析：先设C（acosφ，bsinφ）进而可得四边形ABCD 的面积的表达式整理得4absin
cos3
，进而根据sin
cos3
的范围求得答案．
解答：解：设C（acosφ，bsinφ），则四边形ABCD 的面积=absinφ+abcosφsinφ
=absinφ（1+cosφ）=4absin
cos3
因为sin2
×cos6
=
×3sin2
×cos2
×cos2
×cos2
≤
×（
）4=
．
所以sin
cos
≤
．
所以则四边形ABCD的面积的最大值为：
．
点评：本题主要考查了椭圆的简单性质．本题利用了椭圆的参数方程通过三角函数的性质来解决问题．
cos3，进而根据sincos3的范围求得答案．解答：解：设C（acosφ，bsinφ），则四边形ABCD 的面积=absinφ+abcosφsinφ
=absinφ（1+cosφ）=4absin
cos3因为sin2
×cos6=
×3sin2×cos2×cos2×cos2≤
×（）4=．所以sin
cos≤．所以则四边形ABCD的面积的最大值为：
．点评：本题主要考查了椭圆的简单性质．本题利用了椭圆的参数方程通过三角函数的性质来解决问题．
练习册系列答案
相关题目
=1内一点A(1，1)，则过点A且被该点平分的弦所在直线的方程是_________________________.
=1内一点A（1，1），则过点A且被该点平分的弦所在直线的方程是________．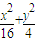
=1按向量a=(t-3,t2)(t∈R)平移后得到曲线E,设曲线E的右焦点为P.
),且
(m∈R),求∠AOB(O为坐标原点)的最大值.
=1内一点A（1，1），则过点A且被该点平分的弦所在直线的方程是 ．