Question

【题目】点与定点的距离和它到直线的距离的比是常数．

（Ⅰ）求点的轨迹的方程；

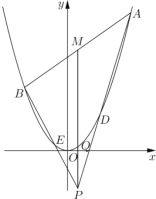
（Ⅱ）过坐标原点的直线交轨迹于，两点，轨迹上异于，的点满足直线的斜率为．

（ⅰ）证明：直线与的斜率之积为定值；

（ⅱ）求面积的最大值．

Answer 1

【答案】（Ⅰ）（Ⅱ）（ⅰ）证明见解析；（ⅱ）．

【解析】

（Ⅰ）根据已知条件列方程，化简后求得轨迹的方程.

（Ⅱ）

（ⅰ）利用点差法，求得，由此证得结论成立.

（ⅱ）利用弦长公式求得，利用点到直线的距离公式求得到直线的距离，由此求得三角形面积的表达式，利用二次函数的性质求得三角形面积的最大值.

（Ⅰ）由已知得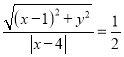，两边平方并化简得，

即点的轨迹的方程为：．

（Ⅱ）（ⅰ）设点，则点，满足， ①

设点，满足， ②

由①－②得：，

∵，，

∴．

（ⅱ）∵，关于原点对称，∴，

设直线，代入曲线化简得：，

设，，由得：，，，

，

点到直线的距离，

∴，

∴，当时，

∴取到最大值．