题目内容
A.不等式 的解集为
的解集为
B.如图,已知 的两条直角边
的两条直角边 的长分别为3cm,4cm,以
的长分别为3cm,4cm,以 为直径的圆与
为直径的圆与 交于点
交于点 ,则
,则 .
.
C.已知圆 的参数方程为
的参数方程为 (
( 为参数)以原点为极点,
为参数)以原点为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 ,则直线
,则直线 与圆
与圆 的交点的直角坐标系为_______
的交点的直角坐标系为_______
A. ;B.
;B. ;C.
;C. 和
和
解析试题分析:A.当 时,原不等式等价于
时,原不等式等价于 ,即
,即 不成立;当
不成立;当 时,原不等式等价于
时,原不等式等价于 ,解得
,解得 ;当
;当 时,原不等式等价于
时,原不等式等价于 ,即
,即 恒成立,所以原不等式的解集为
恒成立,所以原不等式的解集为 .
.
B.在 中,
中, .∵以
.∵以 为直径的圆与
为直径的圆与 交于点
交于点 ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ .
.
C.由题设知,在直角坐标系下,直线 的方程为
的方程为 ,圆
,圆 的方程为
的方程为 .联立方程
.联立方程 ,得
,得 或
或 ,故所求交点的直角坐标为
,故所求交点的直角坐标为 和
和 .
.
考点:1、绝对值不等式的解法;2、与圆有关的比例线段;3、直线与圆的参数方程.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知点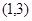 和
和 在直线
在直线 的两侧,则
的两侧,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.不确定 |
如果 ,那么下列不等式一定成立的是( )
,那么下列不等式一定成立的是( )
A. | B. |
C. | D. |
不等式 的解集为
的解集为 ,则实数
,则实数 的值为( )
的值为( )
A. | B. |
C. | D. |
不等式x2+ax+4<0的解集不是空集,则实数a的取值范围是( )
| A.[-4,4] | B.(-4,4) |
| C.(-∞,-4]∪[4,+∞) | D.(-∞,-4)∪(4,+∞) |
不等式 的解集是( )
的解集是( )
A.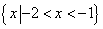 |
B. |
C.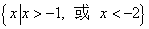 |
D. |
不等式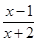 <0的解集为( )
<0的解集为( )
| A.(1,+∞) | B.(-∞,-2) |
| C.(-2,1) | D.(-∞,-2)∪(1,+∞) |
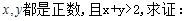

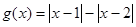 ,则
,则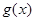 的值域为 ;若关于
的值域为 ;若关于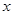 的不等式
的不等式 的解集为空集,则实数
的解集为空集,则实数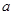 的取值范围是 .
的取值范围是 .