题目内容
4.已知向量$\overrightarrow a=({1,0}),\overrightarrow b=({-2,1})$.(1)若$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$垂直,求k的值;
(2)若$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$平行,求k的值.
分析 (1)利用平面向理坐标运算法则先分别求出$k\overrightarrow a-\overrightarrow b$和$\overrightarrow a+3\overrightarrow b$,再利用$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$垂直,能求出k的值.
(2)利用$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$平行,结合向量平行的性质,能求出k的值.
解答 解:(1)∵向量$\overrightarrow a=({1,0}),\overrightarrow b=({-2,1})$.
∴$k\overrightarrow a-\overrightarrow b$=(k,0)-(-2,1)=(k+2,-1),
$\overrightarrow a+3\overrightarrow b$=(1,0)+(-6,3)=(-5,3),
∵$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$垂直,
∴($k\overrightarrow{a}-\overrightarrow{b}$)•($\overrightarrow{a}+3\overrightarrow{b}$)=-5(k+2)-3=0,
解得$k=-\frac{13}{5}$.
(2)∵$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$平行,
∴$\frac{k+2}{-5}=\frac{-1}{3}$,解得$k=-\frac{1}{3}$.
点评 本题考查平面向量运算法则、向量平行与向量垂直的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.

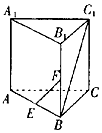 如图所示,在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ABC=90°,点E、F分别是棱AB、BB1的中点,当二面角C1-AA1-B为45o时,直线EF和BC1所成的角为( )
如图所示,在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ABC=90°,点E、F分别是棱AB、BB1的中点,当二面角C1-AA1-B为45o时,直线EF和BC1所成的角为( )| A. | 45o | B. | 60o | C. | 90o | D. | 120o |
| A. | 81种 | B. | 64种 | C. | 36种 | D. | 18种 |
| A. | 在一次试卷分析中,从每个考室中抽取第5号考生的成绩进行统计,不是简单随机抽样 | |||||||||||||||||||
| B. | 对一个样本容量为100的数据分组,各组的频数如下:
| |||||||||||||||||||
| C. | 设产品产量与产品质量之间的线性相关系数为-0.91,这说明二者存在着高度相关 | |||||||||||||||||||
| D. | 通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如表列联表:
|
| A. | 奇函数 | B. | 周期是$\frac{π}{2}$ | ||
| C. | 关于直线$x=\frac{π}{12}$对称 | D. | 关于点$({-\frac{π}{4},0})$对称 |
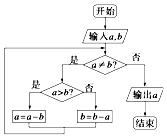 右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.
右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.