题目内容
(14分)已知:函数f(x)=2sinx cosx-cos2x+sin2x
(1)求函数f(x)的最小正周期;
(2)当x∈[0, ]时,求f(x)的值域。
(3)若y=f(x)的图象在[0, m]上恰好有两个点的纵坐标为1,求实数m的取值范围。
(14分)f(x)=sin2x-(cos2x-sin2x)
=sin2x-cos2x
=2(sin2x-cos2x)
=2sin(2x-) …………………………4分
(1)T==2 …………………………6分
(2)0≤x≤ 0≤2x≤π
-≤2x-≤
-≤sin(2x- )≤1
-1≤2sin(2x- )≤2
∴x∈[0, ]时,f(x)的值域为[-1, 2] …………………………10分
2sin(2x- )=1
则 sin(2x-)=
2x- =2kπ+ 或 2x- =2kπ+
2x=2kπ+ 2x=2kπ+π
x=kπ+ x=kπ+
k=0 x= k=0 x=
k=1 x= k=1 x=
∴ m∈[,] ……………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的最大值为
的最大值为 ,最小正周期为
,最小正周期为 .
. 的解析式;
的解析式; 的三条边为
的三条边为 ,
, ,
, ,满足
,满足 ,
,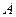 .求:角
.求:角 的值域.
的值域.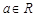 ,函数
,函数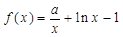 ,
,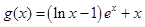 (其中
(其中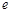 为自然对数的底数).
为自然对数的底数).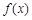 在
在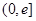 上的单调性;
上的单调性;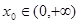 ,使曲线
,使曲线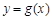 在点
在点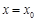 处的切线与
处的切线与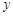 轴垂直? 若存在,
轴垂直? 若存在,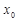 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;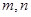 满足
满足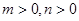 ,求证:
,求证: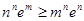 .
. 函数
函数 的定义域为集合B。
的定义域为集合B。 ,求集合
,求集合 ;
; 是“
是“ ”的必要条件,求实数a的取值范围。
”的必要条件,求实数a的取值范围。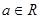 ,函数
,函数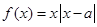 ,
,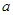 =2时,写出函数
=2时,写出函数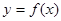 的单调递增区间;
的单调递增区间;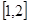 上的最小值;
上的最小值;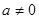 ,函数
,函数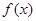 在
在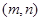 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出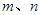 的取值范围(用
的取值范围(用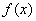 的定义域为
的定义域为 ,且满足对于任意
,且满足对于任意 ,都有
,都有 ,
,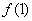 的值; (2)判断
的值; (2)判断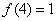 ,
, 且
且 上是增函数,求:
上是增函数,求: 的取值范围。
的取值范围。