题目内容
如图,已知四棱锥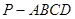 的底面为菱形,
的底面为菱形,
 面
面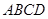 ,且
,且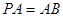 ,
,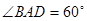 ,
,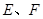 分别是
分别是 的中点.
的中点.
(1)求证: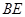 ∥平面
∥平面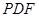 ;
;
(2)过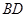 作一平面交棱
作一平面交棱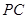 于点
于点 ,若二面角
,若二面角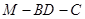 的大小为
的大小为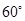 ,求
,求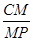 的值.
的值.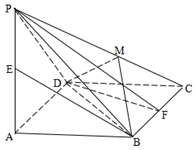
(1)详见解析;(2)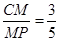 .
.
解析试题分析:(1)问题需要证明的是线面平行,可以考虑通过证明线线平行来证明面面平行,而题中出现了中点,因此可以考虑通过构造三角形中位线来产生平行线:取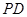 的中点
的中点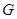 ,连结
,连结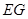 、
、 ,
,
易证四边形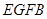 是平行四边形,从而
是平行四边形,从而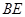 ∥
∥ ,而
,而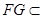 平面
平面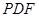 ,
,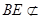 平面
平面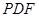 ;(2)根据图形的对称性,可以利用等腰三角形三线合一的性质来构造二面角的平面角,从而利用已知条件中二面角
;(2)根据图形的对称性,可以利用等腰三角形三线合一的性质来构造二面角的平面角,从而利用已知条件中二面角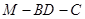 的大小为
的大小为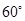 构造含
构造含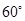 的三角形,进而可以求得线段长度之间的关系:连结
的三角形,进而可以求得线段长度之间的关系:连结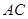 交
交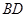 于
于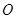 ,连结
,连结 ,易证
,易证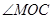 就是二面角
就是二面角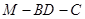 的平面角,
的平面角,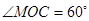 ,
,
不妨设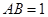 ,可求得
,可求得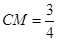 ,从而
,从而 .
.
试题解析:(1)如图,取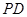 的中点
的中点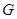 ,连结
,连结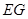 、
、 ,
,
∵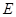 是
是 的中点,∴
的中点,∴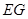 ∥
∥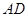 ,且
,且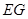
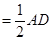 ,又
,又 是菱形
是菱形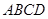 边
边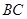 的中点,∴
的中点,∴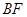 ∥
∥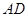 ,且
,且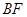
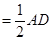 , ∴
, ∴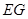 ∥
∥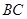 ,且
,且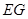
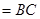 ,四边形
,四边形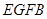 是平行四边形,∴
是平行四边形,∴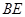 ∥
∥ , 5分
, 5分
而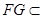 平面
平面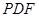 ,
,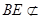 平面
平面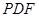 , 6分
, 6分
∴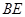 ∥平面
∥平面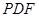 . 7分
. 7分
连结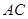 交
交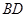 于
于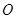 ,连结
,连结 ,∵
,∵
 面
面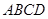 ,∴
,∴

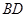 ,
,
即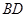

 ,又
,又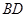

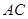 ,且
,且

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
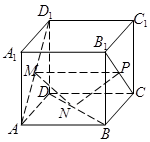
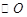 的直径AB=3,点C为
的直径AB=3,点C为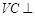 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点. 平面VAC;
平面VAC;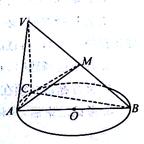
 中,
中, ,
,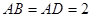 ,
,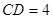 ,点
,点 为线段
为线段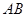 上异于
上异于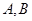 的点,且
的点,且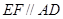 ,沿
,沿 将面
将面 折起,使平面
折起,使平面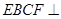 平面
平面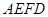 ,如图2.
,如图2.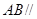 平面
平面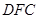 ;
;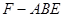 体积最大时,求平面
体积最大时,求平面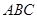 与平面
与平面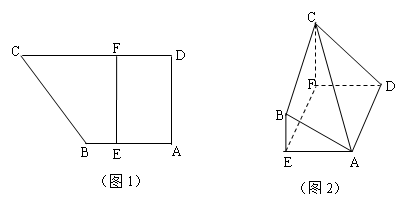
 中,
中, 、
、 分别为
分别为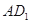 ,
, 中点。
中点。 与
与 所成角的大小;
所成角的大小; 平面
平面 。
。
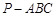 中,点
中,点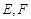 分别是棱
分别是棱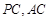 的中点.
的中点. 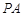 //平面
//平面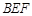 ;
; 平面
平面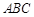 ,
,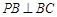 ,求证:
,求证: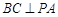 .
.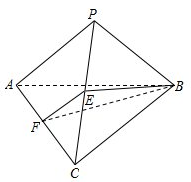
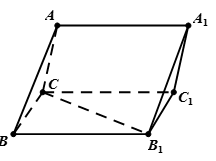
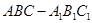 中,侧面
中,侧面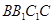 为菱形,
为菱形,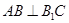 .
.
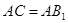 ;
;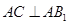 ,
, ,
,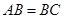 ,求二面角
,求二面角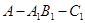 的余弦值.
的余弦值.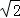 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2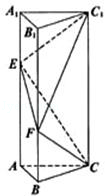
 中
中

 则
则 ▲
▲