题目内容
在△ABC中,向量| OA |
| OB |
| 3 |
| OA |
| OB |
(Ⅰ)求函数f(C)解析式,并求f(C)的单调区间;
(Ⅱ)若△ABC是钝角三角形,且a>0时,f(C)的最小值为-5,求a的值.
分析:本题考查的知识点是平面微量的数量积运算和三角函数的性质,
(1)由向量
=(acos2C, 1),
=(2,
asin2C-a),f(C)=
•
,我们根据向量的数量积运算法则,结合辅助角公式,不难给出函数f(C)解析式,然后对参数a进行分类讨论,可求f(C)的单调区间.
(2)由△ABC是钝角三角形,且a>0,则C∈(
,π)分析函数f(C)的性质,易得当2C+
=
时,函数f(C)有最小值,代入即可求出a值.
(1)由向量
| OA |
| OB |
| 3 |
| OA |
| OB |
(2)由△ABC是钝角三角形,且a>0,则C∈(
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解答:解:(Ⅰ)f(C)=2acos2C+
asin2C-a=
asin2C+acos2C=2asin(2C+
).
∵0<C<π,
∴
<2C+
<
.
若a>0,
当
<2C+
≤
时,即0<C≤
时,
f(C)为增函数,f(C)的单调递增区间是(0,
];
当
<2C+
<
时,即
<C<π时,
f(C)为减函数,f(C)的单调递减区间是(
,π).
若a<0,
当
<2C+
≤
时,即0<C≤
时,
f(C)为减函数,f(C)的单调递减区间是(0,
];
当
<2C+
<
时,即
<C<π时,
f(C)为增函数,f(C)的单调递增区间是(
,π).
(Ⅱ)f(C)=2asin(2C+
),
当C∈(
,π)时,
2C+
∈(
,2π).
当2C+
=
时,
f(C)最小值为-2a=-5,
则a=
| 3 |
| 3 |
| π |
| 6 |
∵0<C<π,
∴
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
若a>0,
当
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
f(C)为增函数,f(C)的单调递增区间是(0,
| π |
| 6 |
当
| π |
| 2 |
| π |
| 6 |
| 13π |
| 6 |
| π |
| 6 |
f(C)为减函数,f(C)的单调递减区间是(
| π |
| 6 |
若a<0,
当
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
f(C)为减函数,f(C)的单调递减区间是(0,
| π |
| 6 |
当
| π |
| 2 |
| π |
| 6 |
| 13π |
| 6 |
| π |
| 6 |
f(C)为增函数,f(C)的单调递增区间是(
| π |
| 6 |
(Ⅱ)f(C)=2asin(2C+
| π |
| 6 |
当C∈(
| π |
| 2 |
2C+
| π |
| 6 |
| 7π |
| 6 |
当2C+
| π |
| 6 |
| 3π |
| 2 |
f(C)最小值为-2a=-5,
则a=
| 5 |
| 2 |
点评:处理三角函数与平面向量的综合题,通常利用向量的数量积等知识,将向量问题转化为三角函数问题来处理.考查综合能力,转化与化归思想,以及分析问题和解决问题的能力.解决本题的关键是,利用两个向量的数量积的坐标形式,将向量问题转化为三角函数问题来处理.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
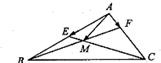 在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使
在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使 如图所示,在△ABC中,D,F分别是AB,AC的中点,BF与CD交于点O,设
如图所示,在△ABC中,D,F分别是AB,AC的中点,BF与CD交于点O,设 (2011•惠州二模)在平面向量中有如下定理:设点O,P,Q,R为同一平面内的点,则P,Q,R三点共线的充要条件是:存在实数t,使
(2011•惠州二模)在平面向量中有如下定理:设点O,P,Q,R为同一平面内的点,则P,Q,R三点共线的充要条件是:存在实数t,使