题目内容
8.已知命题$p:?x>0,x+\frac{2}{x}≥m$;q:m2-4m-5>0.(1)若命题?p是假命题,求m的最大值;
(2)若命题中p,p∨q,p∧q中有两个真命题,一个假命题,求m的取值范围.
分析 (1)对于命题P:利用基本不等式的性质即可得出m的取值范围,若命题?p是假命题,则命题p是真命题,即可得出;
(2)对于命题q:m2-4m-5>0,解得m范围.由命题中p,p∨q,p∧q中有两个真命题,一个假命题,只能:p是真命题,q是假命题,解出即可.
解答 解:(1)命题P:∵x>0,∴$x+\frac{2}{x}$$≥2\sqrt{x•\frac{2}{x}}$=2$\sqrt{2}$,∴m≤2$\sqrt{2}$;
若命题?p是假命题,∴命题p是真命题,∴m$≤2\sqrt{2}$,
∴m的最大值为2$\sqrt{2}$.
(2)对于命题q:m2-4m-5>0,解得m>5或m<-1.
由命题中p,p∨q,p∧q中有两个真命题,一个假命题,
只能:p是真命题,q是假命题,则p,p∨q,是真命题,p∧q是假命题,
可得$\left\{\begin{array}{l}{m≤2\sqrt{2}}\\{-1≤m≤5}\end{array}\right.$,解得-1≤m$≤2\sqrt{2}$.
∴m的取值范围是-1≤m$≤2\sqrt{2}$.
点评 本题考查了复合命题真假的判定方法、一元二次不等式的解法、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.过点P(3,0)有一条直线l,它夹在两条直线l1:2x-y-2=0与l2:x+y+3=0之间的线段恰被点P平分,则直线l方程为( )
| A. | 6x-y-18=0 | B. | 8x-y-24=0 | C. | 5x-2y-15=0 | D. | 8x-3y-24=0 |
3.函数f(x)=3x+x3-3在区间(0,1)内的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
20.空间中,下列命题正确的是( )
| A. | 若a∥α,b∥a,则b∥α | B. | 若a∥α,b∥α,a?β,b?β,则β∥α | ||
| C. | 若α∥β,b∥α,则b∥β | D. | 若α∥β,a?α,则a∥β |
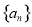 中,已知
中,已知 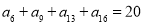 ,则S21等于( )
,则S21等于( )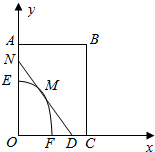 如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.
如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.