题目内容
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
(1)求证:BE∥平面PDA;
(2)若k为线段PB的中点,求证:Ek⊥平面PDB.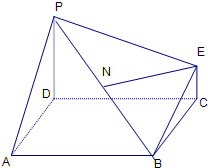
(1)求证:BE∥平面PDA;
(2)若k为线段PB的中点,求证:Ek⊥平面PDB.

(0)证明:∵EC∥PD,PD?平面PDA,EC?平面PDA,∴EC∥平面PDA,同理可得BC∥平面PDA.
∵EC?平面EBC,BC?平面EBC,且EC∩BC=C,∴平面BEC∥平面PDA,
又∵BE?平面EBC,∴BE∥平面PDA.
(2)证明:连接AC与BD交于点F,连接NF,∵F为BD的中点,∴NF∥PD,且NF=
PD.
又EC∥PD,且EC=
PD,∴NF∥EC且NF=EC,∴四边形NFCE为平行四边形,∴NE∥FC.
∵DB⊥AC,PD⊥平面ABCD,AC?面ABCD∴AC⊥PD,
又PD∩BD=D,∴AC⊥面PBD,∴NE⊥面PDB.
∵EC?平面EBC,BC?平面EBC,且EC∩BC=C,∴平面BEC∥平面PDA,
又∵BE?平面EBC,∴BE∥平面PDA.
(2)证明:连接AC与BD交于点F,连接NF,∵F为BD的中点,∴NF∥PD,且NF=
| 0 |
| 2 |
又EC∥PD,且EC=
| 0 |
| 2 |
∵DB⊥AC,PD⊥平面ABCD,AC?面ABCD∴AC⊥PD,
又PD∩BD=D,∴AC⊥面PBD,∴NE⊥面PDB.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.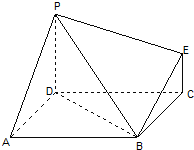 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,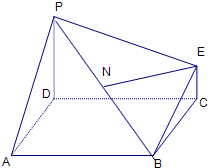 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC, 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.