题目内容
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.(1)求证:BE∥平面PDA;
(2)若平面PBE与平面ABCD所成的二面角为45°,则线段PD是线段AD的几倍?
分析:(1)根据面面垂直的性质,先证明平面BEC∥平面PDA,然后求证:BE∥平面PDA;
(2)延长PE交DC于F,确定二面角PBE与平面ABCD平面角,建立方程求解PD和AD的关系.
(2)延长PE交DC于F,确定二面角PBE与平面ABCD平面角,建立方程求解PD和AD的关系.
解答:解:(1)∵EC∥PD,ABCD为正方形,
∴BC∥AD,
∵EC∩BC=C,
∴平面BEC∥平面PDA,
又BE?平面BEC,
∴BE∥平面PDA.
(2)延长PE交DC于F,
∵PD=2EC,
∴E,C分别是PF和DF的中点,
连结BF,
则∠DBF=90°,
∵PD⊥平面ABCD,
∴BF⊥平面PBD,
∴∠PBD是平面PBE与平面ABCD所成的二面角,
即∠PBD=45°.
∵ABCD为正方形,则BD=
AD,
∴此时PD=BD=
AD,
即线段PD是线段AD的
倍.
∴BC∥AD,
∵EC∩BC=C,
∴平面BEC∥平面PDA,
又BE?平面BEC,
∴BE∥平面PDA.
(2)延长PE交DC于F,

∵PD=2EC,
∴E,C分别是PF和DF的中点,
连结BF,
则∠DBF=90°,
∵PD⊥平面ABCD,
∴BF⊥平面PBD,
∴∠PBD是平面PBE与平面ABCD所成的二面角,
即∠PBD=45°.
∵ABCD为正方形,则BD=
| 2 |
∴此时PD=BD=
| 2 |
即线段PD是线段AD的
| 2 |
点评:本题主要考查线面平行的判断以及二面角的应用,利用面面平行的性质是解决本题的关键,考查学生的推理能力.

练习册系列答案
相关题目
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.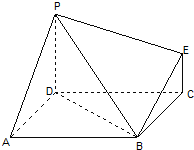 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,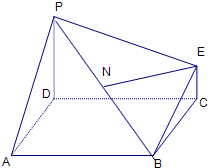 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,