题目内容
【题目】函数![]() 的部分图象如图所示,又函数
的部分图象如图所示,又函数![]() .
.
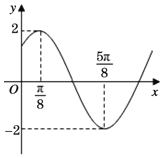
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)设![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,又
,又![]() ,且锐角
,且锐角![]() 满足
满足![]() ,若
,若![]() ,
,![]() 为
为![]() 边的中点,求
边的中点,求![]() 的周长.
的周长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用函数图象求得![]() 、
、![]() 的值,再由函数
的值,再由函数![]() 的图象过点
的图象过点![]() 求得
求得![]() 的值,进而可得出
的值,进而可得出![]() ,由此可得出
,由此可得出![]() ,然后解不等式
,然后解不等式![]() ,即可得出函数
,即可得出函数![]() 的单调递增区间;;
的单调递增区间;;
(2)由![]() 可求得角
可求得角![]() 的值,利用正弦定理边角互化思想得出
的值,利用正弦定理边角互化思想得出![]() ,结合余弦定理可求得
,结合余弦定理可求得![]() 、
、![]() ,进而可判断出
,进而可判断出![]() 为直角三角形,且角
为直角三角形,且角![]() 为直角.可计算出
为直角.可计算出![]() 的长,进而可求得
的长,进而可求得![]() 的周长.
的周长.
(1)由函数![]() 的部分图象可得
的部分图象可得![]() ,
,
![]() ,即
,即![]() ,则
,则![]() ,
,
又函数![]() 的图象过点
的图象过点![]() ,则
,则![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,
即![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,
,
所以函数![]() 的单调增区间为
的单调增区间为![]() ;
;
(2)由![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,得
,得![]() ,
,
又![]() ,由正弦定理得
,由正弦定理得![]() ,①
,①
由余弦定理,得![]() ,即
,即![]() ,②
,②
由①②解得![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() 为直角三角形,且角
为直角三角形,且角![]() 为直角.
为直角.
故![]() ,所以
,所以![]() 的周长为
的周长为![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目