题目内容
【题目】已知在极坐系中,点![]() 绕极点
绕极点![]() 顺时针旋转角
顺时针旋转角![]() 得到点
得到点![]() .以
.以![]() 为原点,极轴为
为原点,极轴为![]() 轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线
轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到曲线
得到曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)14.
;(2)14.
【解析】
(1)求得点![]() 绕极点
绕极点![]() 顺时针旋转
顺时针旋转![]() 得到点
得到点![]() ,代入曲线
,代入曲线![]() 上,结合极坐标与直角坐标的互化公式,即可求求解;
上,结合极坐标与直角坐标的互化公式,即可求求解;
(2)求得![]() 的直角坐标,设
的直角坐标,设![]() 的参数方程为
的参数方程为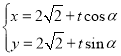 (
(![]() 为参数),代入
为参数),代入![]() ,利用参数的几何意义和三角函数性质,即可求解.
,利用参数的几何意义和三角函数性质,即可求解.
(1)设![]() 为曲线
为曲线![]() 是任意一点,
是任意一点,
则点![]() 绕极点
绕极点![]() 顺时针旋转
顺时针旋转![]() 得到点
得到点![]() 在曲线
在曲线![]() 上,
上,
又由![]() 的直线坐标方程为
的直线坐标方程为![]() ,代入可得
,代入可得![]() ,
,
整理![]() ,所以
,所以![]() ,
,
即曲线![]() 的方程为
的方程为![]() .
.
(2)由点![]() 的极坐标为
的极坐标为![]() ,可得
,可得![]() 的直角坐标为
的直角坐标为 ![]() ,
,
设![]() 的参数方程为
的参数方程为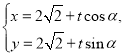 (
(![]() 为参数),
为参数),
代入![]() ,整理后可得
,整理后可得![]() ,
,
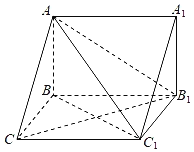
所以![]() ,
,
当且仅当![]() 或
或![]() 时取等号,此时
时取等号,此时![]() ,符合条件,
,符合条件,
故![]() 的最小值为14.
的最小值为14.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
【题目】2019年郑开国际马拉松比赛,于2019年3月31日在郑州、开封举行.某学校本着“我运动,我快乐,我锻炼,我提高”精神,积极组织学生参加比赛及相关活动,为了了解学生的参与情况,从全校学生中随机抽取了150名学生,对是否参与的情况进行了问卷调查,统计数据如下:
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
(1)根据上表说明,能否有97.5%的把握认为参与马拉松赛事与性别有关?
(2)现从参与问卷调查且参与赛事的学生中,采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动,
①求男、女学生各选取多少人;
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍,求恰好选到2名男生的概率.
附:参考公式:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |