已知个正数排成一个n行n列的数阵: 第1列第2列第3列 - 第n列第1行 - 第2行 - 第3行 - - 第n行 - 其中表示该数阵中位于第i行第k列的数.已知该数阵中各行的数依次成等比数列.各列的数依次成公比为2的等比数列.已知a2,3=8.a3,4=20. (1)求, (2)设能被3整除. 题目和参考答案——青夏教育精英家教网——

题目内容

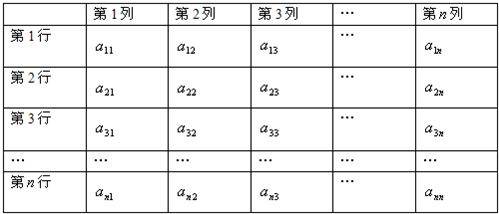
已知个正数排成一个n行n列的数阵：

第1列第2列第3列 … 第n列

第1行 …

第2行 …

第3行 …

…

第n行 …

其中表示该数阵中位于第i行第k列的数，已知该数阵中各行的数依次成等比数列，各列的数依次成公比为2的等比数列，已知a_2,3=8，a_3,4=20.

（1）求；

（2）设能被3整除.

同下

解析:

（1）由题意，，

故第1行公差d=1，所以………………6分

（2）同（1）可得，

所以

两式相减，得

所以能被3整除. ………………16分

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

a²（n≥4，n∈N^*）个正数排成一个n行n列的数阵：

其中a_ik（1≤i≤n，1≤k≤n，k∈N^*）表示该数阵中位于第i行第k列的数，已知该数阵每一行的数成等差数列，每一列的数成公比为2的等比数列，a₂₃=8，a₃₄=20．
（1）求a₁₁和a_ik；
（2）设A_n=a_1n+a_2（n-1）+a_3（n-2）+…+a_n1，是否存在整数p使得不等式A_n≥11n+p对任意的n∈N^*恒成立，如果存在，求出p的最大值；如果不存在，请说明理由．

（文科）已知n²（n≥4且n∈N*）个正数排成一个n行n列的数阵：
          第1列    第2列    第3列   …第n列
第1行     a_1，1a_1，2a_1，3…a_1，n
第2行     a_2，1a_2，2a_2，3…a_2，n
第3行     a_3，1a_3，2a_3，3…a_3，n
…
第n行     a_n，1a_n，2a_n，3…a_n，n
其中a_i，k（i，k∈N*，且1≤i≤n，1≤k≤n）表示该数阵中位于第i行第k列的数，已知该数阵中各行的数依次成等比数列，各列的数依次成公比为2的等比数列，已知a_2，3=8，a_3，4=20．
（1）求a_1，1a_2，2；
（2）设A_n=a_1，n+a_2，n-1+a_3，n-2+…+a_n，1求证：A_n+n能被3整除．

（本小题满分16分）已知个正数排成一个n行n列的数阵：

第1列第2列第3列 … 第n列

第1行 …

第2行 …

第3行 …

…

第n行 …

其中表示该数阵中位于第i行第k列的数，已知该数阵中各行的数依次成等比数列，各列的数依次成公比为2的等比数列，已知a_2,3=8，a_3,4=20.

（1）求；（2）设能被3整除.

（本小题满分16分）已知个正数排成一个n行n列的数阵：

第1列第2列第3列 … 第n列

第1行 …

第2行 …

第3行 …

…

第n行 …

其中表示该数阵中位于第i行第k列的数，已知该数阵中各行的数依次成等比数列，各列的数依次成公比为2的等比数列，已知a_2,3=8，a_3,4=20.

（1）求；（2）设能被3整除.