题目内容

【题目】已知圆与直线相切于点，且经过点，求圆的方程.

【答案】x2＋y2－10x－9y＋39＝0

【解析】试题分析：本题解法有4种,①由直线与圆相切于点A可设方程,再过点B可求出,即求出圆的方程.②可以设圆的标准方程,由圆心和切点连线与切线垂直且圆过A,B两点可找到三个关系式求出从而得到圆的方程.③可设所求圆的方程的一般式,写出圆心坐标,由圆心和切点连线与切线垂直且圆过A,B两点可找到三个关系式求出从而得到圆的方程.④设出圆心坐标,由几何意义可以由圆心和切点连线与切线垂直先求出直线CA方程,再由A,B坐标求出直线AB的方程,由AB的垂直平分线与CA相交于点C,再CA的长度即为圆的半径从而得到圆的方程.

试题解析：

法一：由题意可设所求的方程为，又因为此圆过点，将坐标代入圆的方程求得，所以所求圆的方程为.

法二：设圆的方程为，

则圆心为，由，得

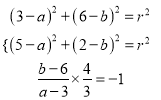解得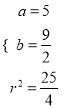

所以所求圆的方程为.

法三：设圆的方程为，由， , 在圆上，得

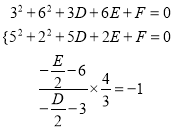解理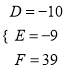

所以所求圆的方程为.

法四：设圆心为C，则，又设AC与圆的另一交点为P，则CA的方程为，

即.

又因为，

所以，所以直线BP的方程为.

解方程组得所以．

所以圆心为AP的中点，半径为,

所以所求圆的方程为.

练习册系列答案
相关题目

【题目】如图1，在路边安装路灯，路宽为，灯柱长为米，灯杆长为1米，且灯杆与灯柱成角，路灯采用圆锥形灯罩，其轴截面的顶角为，灯罩轴线与灯杆垂直．

⑴设灯罩轴线与路面的交点为，若米，求灯柱长；

⑵设米，若灯罩截面的两条母线所在直线一条恰好经过点，另一条与地面的交点为（如图2）

（图1） （图2）

（ⅰ）求的值；（ⅱ）求该路灯照在路面上的宽度的长．

【题目】已知函数f（x）的导数f′（x）=a（x+1）（x﹣a），若f（x）在x=a处取到极大值，则a的取值范围是 ．

【题目】设函数f（x）= （a∈R）
（1）若f（x）在x=0处取得极值，确定a的值，并求此时曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若f（x）在[3，+∞）上为减函数，求a的取值范围．

【题目】如图，四边形是等腰梯形， ， ， ，在梯形中， ，且， 平面.

（1）求证：面面；

（2）若二面角的大小为，求几何体的体积.

【题目】定义max{a，b}表示实数a，b中的较大的数．已知数列{an}满足a1=a（a＞0），a2=1，an+2= （n∈N），若a2015=4a，记数列{an}的前n项和为Sn ， 则S2015的值为 ．

【题目】已知函数f（x）=ax+x2﹣xlna（a＞0且a≠1）
（1）求函数f（x）在点（0，f（0））处的切线方程；
（2）求函数f（x）单调区间；
（3）若存在x1 ， x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1（e是自然对数的底数），求实数a的取值范围．

【题目】已知三棱锥A﹣BPC中，AP⊥PC，AC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．

（1）求证：BC⊥平面APC；
（2）若BC=3，AB=10，求三棱锥B﹣MDC的体积VB﹣MDC ．

【题目】已知数列{an}满足a1=0，an+1=an+2 +1
（1）求证数列{ }是等差数列，并求出an的通项公式；
（2）若bn= ，求数列{b}的前n项的和Tn ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网