题目内容
11．设集合A={x|-3≤2x-1≤3}，集合B为函数y=lg（x-1）的定义域，则A∩B=（1，2]．分析 由对数式的真数大于0求得B，然后直接利用交集运算得答案．
解答 解：由x-1＞0，得x＞1，
∴B=（1，+∞），
又A={x|-3≤2x-1≤3}=[-1，2]，
∴A∩B=（1，2]．
故答案为：（1，2]．
点评 本题考查交集及其运算，考查了函数定义域的求法，是基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1．下列关系式正确的是（ ）
| A． | 0∉Z | B． | ∅⊆{0} | C． | ∅∈{0} | D． | 0∈∅ |
2．设函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-a，}&{x＜1}\\{4（x-a）（x-2a），}&{x≥1}\end{array}\right.$，若f（x）恰有2个零点，则实数a的取值范围是（ ）
| A． | a≥2 | B． | $\frac{1}{2}$≤a＜1 | C． | $\frac{1}{2}$＜a＜1 | D． | a≥2或$\frac{1}{2}$≤a＜1 |
19．如果f（x）=$\frac{1}{2}$（m-2）x2+（n-8）x+1（m＞2，n＞0）在[$\frac{1}{2}，2$]上单调递减，则$\frac{1}{m}$+$\frac{1}{n}$的最小值为（ ）
| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{\sqrt{2}}{6}$ | C． | $\frac{3+2\sqrt{2}}{12}$ | D． | $\frac{3-2\sqrt{2}}{12}$ |
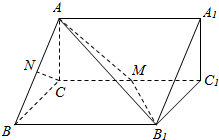如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，CC1=4，M是棱CC1的中点．
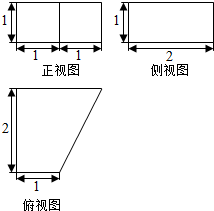一个几何体的三视图如图所示：