题目内容
11.若有穷数列{an}(n≥3)同时满足:(1)$\sum_{k=1}^{n}$ak=0;(2)$\sum_{k=1}^{n}$|ak|=1;则称数列{an}为n阶好数列.
给出以下命题(以下数列项数都大于或等于3):
①不存在有穷常数列,它是好数列;
②存在等差数列,它是好数列;
③若有穷等比数列{an}是2k阶好数列(k≥2),则它的公比只能等于-l;
④存在各项非负的2013阶好数列.
以上所有正确命题的序号为①②③.
分析 ①假设存在有穷常数列{c},它是好数列,则nc=0,解得c=0,而不满足$\sum_{k=1}^{n}$|ak|=1,即可判断出正误;
②例如:数列-$\frac{1}{2}$,0,$\frac{1}{2}$,是等差数列,为好数列,即可判断出正误.
③有穷等比数列{an}是2k阶好数列(k≥2),则必然q<0,由$\sum_{k=1}^{n}$ak=0,则a1×$\frac{1-{q}^{2k}}{1-q}$=0,解得q=-1.
④不可能存在各项非负的2013阶好数列,否则$\sum_{k=1}^{n}$ak=0不满足,即可判断出正误.
解答 解:①假设存在有穷常数列{c},它是好数列,则nc=0,解得c=0,而不满足$\sum_{k=1}^{n}$|ak|=1,因此不存在有穷常数列,它是好数列,正确.
②例如:数列-$\frac{1}{2}$,0,$\frac{1}{2}$,是等差数列,为好数列,正确.
③有穷等比数列{an}是2k阶好数列(k≥2),则必然q<0,由$\sum_{k=1}^{n}$ak=0,则a1×$\frac{1-{q}^{2k}}{1-q}$=0,解得q2k=1,则q=-1.
因此它的公比只能等于-l,正确;
④不可能存在各项非负的2013阶好数列,否则$\sum_{k=1}^{n}$ak=0不满足,因此不正确.
故答案为:①②③.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、新定义,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
1.设圆x2+y2-2x-2y-2=0的圆心为C,直线l过(0,3)与圆C交于A,B两点,若$|{AB}|=2\sqrt{3}$,则直线l的方程为( )
| A. | 3x+4y-12=0或4x-3y+9=0 | B. | 3x+4y-12=0或x=0 | ||
| C. | 4x-3y+9=0或x=0 | D. | 3x-4y+12=0或4x+3y+9=0 |
19.已知函数f(x)=$\left\{\begin{array}{l}{3x+3(x≤-1)}\\{f(x-1)+1(x>-1)}\end{array}\right.$方程f(x)=x+1的解从小到大排成一个数列{an},该数列的前n项的和为Sn,则$\frac{2{S}_{n+3}+10}{n}$的最小值为( )
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
16.某公司新招聘8名员工,随机平均分配给下属的甲、乙两个部门,则事件“两名英语翻译人员不在同一部门,另外三名电脑编程人员也不在同一部门”发生的概率为( )
| A. | $\frac{18}{35}$ | B. | $\frac{15}{35}$ | C. | $\frac{12}{35}$ | D. | $\frac{9}{35}$ |
20.把函数$f(x)=\sqrt{2}sin(2x-\frac{π}{4})$的图象上每个点的横坐标扩大到原来的4倍,再向左平移$\frac{π}{3}$,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
| A. | $[-\frac{5π}{6},\frac{7π}{6}]$ | B. | $[\frac{7π}{6},\frac{19π}{6}]$ | C. | $[-\frac{2π}{3},\frac{4π}{3}]$ | D. | $[-\frac{17π}{6},-\frac{5π}{6}]$ |
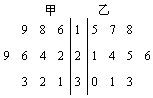 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.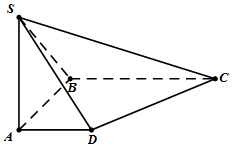 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.