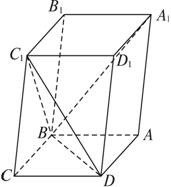
题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
连结AC,交DB于O,连结C1O,易得△C1BC≌△C1DC ∴C1B=C1D 又O为BD中点 ∴C1O⊥BD 又BD⊥AC ∴BD⊥面AA1C1C ∴C1C⊥BD |
(2) |
∠C1DC为二面角C1-BD-C的平面角,作C1H⊥DC于H 在△C1BC中,BC=2,C1C= ∴C1B= ∵∠OCB= ∴OB= ∴C1O2=C1B2-OB2= ∴C1O= ∴C1O=C1C ∴H为OC的中点 ∴OH= ∴cos∠C1OC= ∴∠C1OC,即二面角C1-BD-C的平面角大小为arccos |
(3) |
连结A1C,已知,BD⊥平面AA1C1C ∴BD⊥A1C 当 ∴A1C⊥平面C1BD |

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

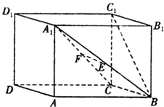 如图所示,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长为a,∠ABC=60°,E、F分别是A1B、A1C的中点.
如图所示,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长为a,∠ABC=60°,E、F分别是A1B、A1C的中点.