题目内容
已知圆 :
: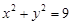 ,点
,点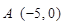 ,直线
,直线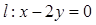 .
.

(1)求与圆 相切,且与直线
相切,且与直线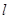 垂直的直线方程;
垂直的直线方程;
(2)在直线 上(
上(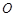 为坐标原点),存在定点
为坐标原点),存在定点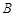 (不同于点
(不同于点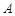 ),满足:对于圆
),满足:对于圆 上的任一点
上的任一点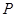 ,都有
,都有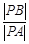 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点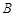 的坐标.
的坐标.
 :
: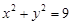 ,点
,点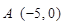 ,直线
,直线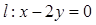 .
.
(1)求与圆
 相切,且与直线
相切,且与直线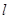 垂直的直线方程;
垂直的直线方程;(2)在直线
 上(
上(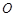 为坐标原点),存在定点
为坐标原点),存在定点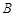 (不同于点
(不同于点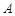 ),满足:对于圆
),满足:对于圆 上的任一点
上的任一点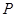 ,都有
,都有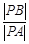 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点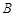 的坐标.
的坐标.(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析试题分析:(1)根据所求直线与已知直线垂直,可设出直线方程,再根据直线与圆相切,所以有
 (其中
(其中 表示圆心到直线的距离),可得到直线方程;
表示圆心到直线的距离),可得到直线方程; (2)方法一:假设存在这样的点
 ,由于
,由于 的位置不定,所以首先考虑特殊位置,①
的位置不定,所以首先考虑特殊位置,① 为圆
为圆 与
与 轴左交点或②
轴左交点或② 为圆
为圆 与
与 轴右交点这两种情况,由于对于圆
轴右交点这两种情况,由于对于圆 上的任一点
上的任一点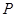 ,都有
,都有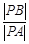 为一常数,所以①②两种情况下的
为一常数,所以①②两种情况下的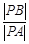 相等, 可得到
相等, 可得到 ,然后证明在一般的
,然后证明在一般的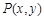 下,
下, 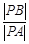 为一常数.
为一常数. 方法二:设出
 ,根据对于圆
,根据对于圆 上的任一点
上的任一点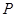 ,都有
,都有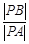 为一常数,设出
为一常数,设出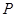 以及该常数
以及该常数 ,通过
,通过 ,代入
,代入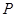 的坐标化简,转化为恒成立问题求解.
的坐标化简,转化为恒成立问题求解.试题解析:(1)已知直线变形为为
 ,因为所求直线与已知直线垂直,
,因为所求直线与已知直线垂直,所以设所求直线方程为
 ,即
,即 .
.由直线与圆相切,可知
 ,其中
,其中 表示圆心到直线的距离,
表示圆心到直线的距离,则
 ,得
,得 ,故所求直线方程为
,故所求直线方程为 .
. (2)假设存在这样的点
 ,
,当
 为圆
为圆 与
与 轴左交点
轴左交点 时,
时,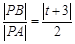 ,
,当
 为圆
为圆 与
与 轴右交点
轴右交点 时,
时,
依题意,
 ,解得
,解得 (舍去),或
(舍去),或 .
.下面证明:点
 对于圆
对于圆 上任一点
上任一点 ,都有
,都有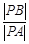 为一常数.
为一常数.设
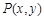 ,则
,则 .
. ,
,从而
 为常数.
为常数. 方法2:假设存在这样的点
 ,使得
,使得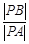 为常数
为常数 ,则
,则 ,
,设
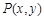 于是
于是 ,由于
,由于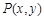 在圆上,所以
在圆上,所以 ,代入得,
,代入得,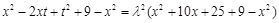 ,
,即
 对
对 恒成立,
恒成立,所以
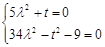 ,解得
,解得 或
或 (舍去),
(舍去),故存在点
 对于圆
对于圆 上任一点
上任一点 ,都有
,都有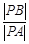 为一常数
为一常数 .
.
练习册系列答案
相关题目
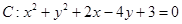 .
.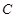 的切线在
的切线在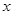 轴和
轴和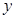 轴上的截距相等,且截距不为零,求此切线的方程;
轴上的截距相等,且截距不为零,求此切线的方程;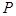 向该圆引一条切线,切点为
向该圆引一条切线,切点为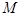 ,
,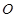 为坐标原点,且有
为坐标原点,且有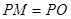 ,求使
,求使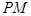 的长取得最小值的点
的长取得最小值的点 中,若圆
中,若圆 上存在
上存在 ,
, 两点关于点
两点关于点 成中心对称,则直线
成中心对称,则直线 的方程为 .
的方程为 . 、
、 为⊙
为⊙ 的切线,
的切线, 、
、 分别为切点,
分别为切点, 为⊙
为⊙ ,则
,则 .
.
 在点
在点 处的切线与圆
处的切线与圆 (
( 相切,则
相切,则 的值为_______.
的值为_______. 与圆
与圆 的位置关系是( )
的位置关系是( )