题目内容
19.设a,b∈R,求证:a2+b2+$\frac{7}{4}$>ab+2a+$\frac{b}{2}$.分析 通过变形可知(a2+b2+$\frac{7}{4}$)-(ab+2a+$\frac{b}{2}$)=$\frac{1}{2}$(2a2+2b2+$\frac{7}{2}$-2ab-4a-b)=$\frac{1}{2}$[(a-b)2+(a-2)2+(b-$\frac{1}{2}$)2-$\frac{3}{4}$],数形结合即得结论.
解答 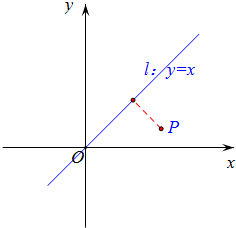 证明:(a2+b2+$\frac{7}{4}$)-(ab+2a+$\frac{b}{2}$)
证明:(a2+b2+$\frac{7}{4}$)-(ab+2a+$\frac{b}{2}$)
=$\frac{1}{2}$(2a2+2b2+$\frac{7}{2}$-2ab-4a-b)
=$\frac{1}{2}$[(a2-2ab+b2)+(a2-4a+4)+(${b}^{2}-b+\frac{1}{4}$)-$\frac{3}{4}$]
=$\frac{1}{2}$[(a-b)2+(a-2)2+(b-$\frac{1}{2}$)2-$\frac{3}{4}$],
而(a-b)2+(a-2)2+(b-$\frac{1}{2}$)2表示点P(2,$\frac{1}{2}$)到直线l:y=x的距离,
利用点到直线的距离公式可知d=$\frac{2-\frac{1}{2}}{\sqrt{2}}$=$\frac{3}{2\sqrt{2}}$,
∵$\frac{3}{2\sqrt{2}}$>$\frac{3}{4}$,
∴(a2+b2+$\frac{7}{4}$)-(ab+2a+$\frac{b}{2}$)>0,
∴a2+b2+$\frac{7}{4}$>ab+2a+$\frac{b}{2}$.
点评 本题考查不等式的证明,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
9.已知全集U={1,2,3,4,5},集合A={2,3,4},B={1,4},则(∁UA)∪B为( )
| A. | {1} | B. | {1,5} | C. | {1,4} | D. | {1,4,5} |
10.y=f(x)在(0,+∞)上是减函数,则f(a2-a+2)与f($\frac{7}{4}$)的大小关系是( )
| A. | f(a2-a+2)≤f($\frac{7}{4}$) | B. | f(a2-a+2)≥f($\frac{7}{4}$) | C. | f(a2-a+2)=f($\frac{7}{4}$) | D. | 不确定 |
7.函数f(x)=x+$\frac{4}{x}$的值域是( )
| A. | [4,+∞) | B. | (4,+∞) | C. | R | D. | (-∞,-4]∪[4,+∞) |
14.若0<x<$\frac{π}{2}$,则x与sinx的大小关系是( )
| A. | x>sinx | B. | x<sinx | C. | x≥sinx | D. | x≤sinx |
8.函数f(x)=x2+x-b2的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数 |
9.已知方程|sinx|-ax=0在区间(0,+∞)上有且仅有两根x1,x2,且x1<x2,下列选项中正确的是( )
| A. | x2=tanx2 | B. | x1=tanx1 | C. | (1+2x2)tan2x2=1 | D. | (1+2x1)tanx1=1 |