题目内容
已知椭圆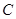 :
: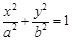 (
(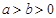 )过点
)过点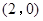 ,且椭圆
,且椭圆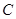 的离心率为
的离心率为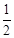 .
.
(Ⅰ)求椭圆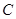 的方程;
的方程;
(Ⅱ)若动点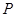 在直线
在直线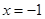 上,过
上,过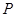 作直线交椭圆
作直线交椭圆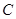 于
于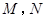 两点,且
两点,且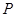 为线段
为线段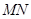 中点,再过
中点,再过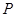 作直线
作直线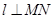 .证明:直线
.证明:直线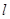 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
(Ⅰ)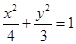 (Ⅱ)直线
(Ⅱ)直线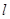 恒过定点
恒过定点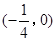
解析试题分析:(Ⅰ)点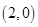 在椭圆上,将其代入椭圆方程,又因为
在椭圆上,将其代入椭圆方程,又因为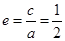 ,且
,且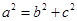 ,解方程组可得
,解方程组可得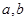 。(Ⅱ)点
。(Ⅱ)点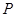 在直线
在直线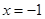 上,则可得
上,则可得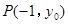 。当直线
。当直线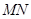 的斜率存在时设斜率为
的斜率存在时设斜率为 ,得到直线
,得到直线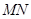 方程,联立方程消掉
方程,联立方程消掉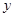 得关于
得关于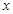 的一元二次方程。再根据韦达定理可得根与系数的关系。因为
的一元二次方程。再根据韦达定理可得根与系数的关系。因为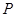 为
为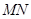 中点,根据点
中点,根据点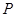 的横坐标解得
的横坐标解得 。因为
。因为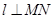 故可得直线
故可得直线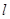 的斜率,及其含参数
的斜率,及其含参数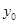 的方程。分析可得直线
的方程。分析可得直线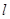 是否恒过定点。注意还要再讨论当直线
是否恒过定点。注意还要再讨论当直线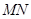 的斜率不存在的情况。
的斜率不存在的情况。
试题解析:解:(Ⅰ)因为点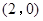 在椭圆
在椭圆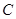 上,所以
上,所以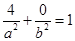 ,
,
所以 , 1分
, 1分
因为椭圆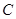 的离心率为
的离心率为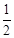 ,所以
,所以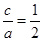 ,即
,即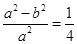 , 2分
, 2分
解得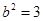 , 4分
, 4分
所以椭圆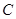 的方程为
的方程为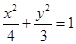 . 5分
. 5分
(Ⅱ)设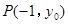 ,
,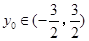 ,
,
①当直线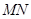 的斜率存在时,设直线
的斜率存在时,设直线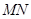 的方程为
的方程为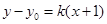 ,
,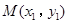 ,
,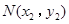 ,
,
由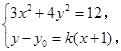 得
得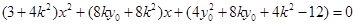 , 7分
, 7分
所以 , 8分
, 8分
因为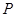 为
为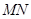 中点,所以
中点,所以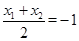 ,即
,即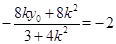 .
.
所以 , 9分
, 9分
因为直线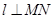 ,所以
,所以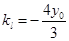 ,
,
所以直线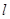 的方程为
的方程为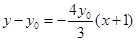 ,即
,即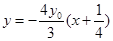 ,
,
显然直线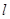 恒过定点
恒过定点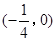 . 11分
. 11分
②当直线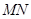 的斜率不存在时,直线
的斜率不存在时,直线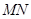 的方程为
的方程为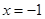 ,
,
此时直线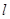 为
为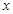 轴,也过点
轴,也过点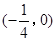 . 13分
. 13分
综上所述直线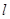 恒过定点
恒过定点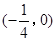 . 14
. 14

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
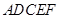 关于直线
关于直线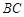 对称(如图(1)),
对称(如图(1)),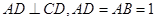 ,
,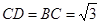 ,将此图形沿
,将此图形沿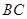 折叠成直二面角,连接
折叠成直二面角,连接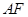 、
、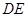 得到几何体(如图(2))
得到几何体(如图(2))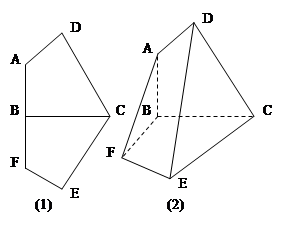
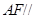 平面
平面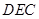 ;
; 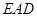 与平面
与平面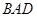 的所成角的正切值.
的所成角的正切值. :
: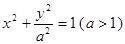 的离心率为
的离心率为 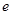 ,点
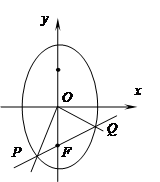
,点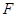 为其下焦点,点
为其下焦点,点 为坐标原点,过
为坐标原点,过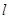 :
: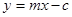 (其中
(其中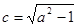 )与椭圆
)与椭圆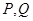 两点,且满足:
两点,且满足: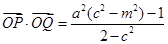 .
.
 表示
表示 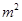 ;
;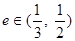 ,求
,求 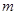 的取值范围.
的取值范围.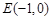 和
和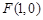 ,圆
,圆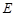 是以
是以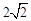 的圆,点
的圆,点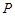 是圆
是圆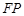 的垂直平分线
的垂直平分线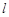 和半径
和半径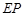 所在的直线交于点
所在的直线交于点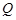 .
.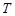 ;
; ,
,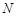 是曲线
是曲线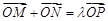 (
( 为坐标原点),求实数
为坐标原点),求实数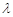 的取值范围.
的取值范围.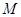 :
: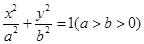 经过如下五个点中的三个点:
经过如下五个点中的三个点: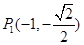 ,
,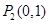 ,
,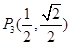 ,
,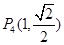 ,
,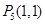 .
. 为椭圆
为椭圆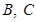 为椭圆
为椭圆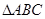 的外部,且
的外部,且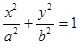
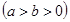 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.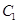 :
: 的离心率为
的离心率为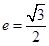 且与双曲线
且与双曲线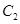 :
: 有共同焦点.
有共同焦点.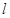 ,求
,求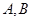 ,过椭圆
,过椭圆 作
作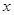 轴的垂线交
轴的垂线交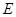 ,若
,若 点满足
点满足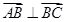 ,
,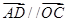 ,连结
,连结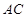 交
交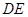 于点
于点 ,求证:
,求证: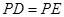 .
.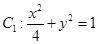 ,椭圆
,椭圆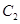 以
以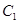 的长轴为短轴,且与
的长轴为短轴,且与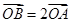 ,求直线
,求直线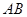 的方程.
的方程.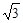 的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.