题目内容
已知椭圆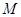 :
: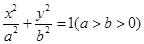 经过如下五个点中的三个点:
经过如下五个点中的三个点: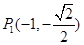 ,
,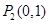 ,
,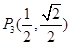 ,
,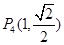 ,
,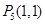 .
.
(Ⅰ)求椭圆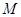 的方程;
的方程;
(Ⅱ)设点 为椭圆
为椭圆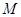 的左顶点,
的左顶点,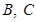 为椭圆
为椭圆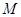 上不同于点
上不同于点 的两点,若原点在
的两点,若原点在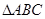 的外部,且
的外部,且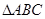 为直角三角形,求
为直角三角形,求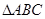 面积的最大值.
面积的最大值.
(Ⅰ)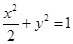 ;(Ⅱ)
;(Ⅱ)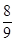
解析试题分析:(Ⅰ)因为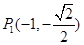 和
和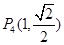 关于原点对称,由椭圆的对称性可知
关于原点对称,由椭圆的对称性可知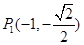 和
和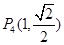 在椭圆上。因为
在椭圆上。因为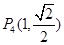 在椭圆上则
在椭圆上则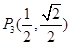 和
和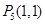 不在椭圆上。所以
不在椭圆上。所以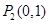 在椭圆上。解方程组可得
在椭圆上。解方程组可得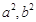 的值。(Ⅱ)需讨论哪个角为直角只讨论
的值。(Ⅱ)需讨论哪个角为直角只讨论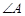 和
和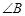 即可,因为点
即可,因为点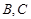 的位置没有固定,
的位置没有固定,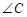 和
和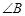 的情况相同。如当
的情况相同。如当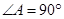 时,设直线
时,设直线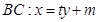 ,联立方程消去消去
,联立方程消去消去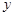 得关于
得关于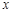 的一元二次方程,由韦达定理得根与系数的关系。根据
的一元二次方程,由韦达定理得根与系数的关系。根据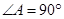 ,则直线垂直其斜率相乘等于
,则直线垂直其斜率相乘等于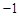 ,列式计算可得
,列式计算可得 ,
,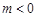 则说明原点在
则说明原点在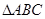 的外部,符合条件,否则不符合条件舍掉。在求
的外部,符合条件,否则不符合条件舍掉。在求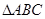 面积时若采用先求弦
面积时若采用先求弦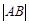 再求点
再求点 到
到 的距离最后求面积的方法计算过于繁琐,所以求
的距离最后求面积的方法计算过于繁琐,所以求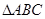 的面积时可用分割法,计算较简单。
的面积时可用分割法,计算较简单。
试题解析:解:(Ⅰ)由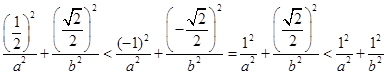 知,
知,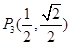 和
和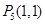 不在椭圆
不在椭圆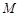 上,即椭圆
上,即椭圆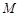 经过
经过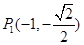 ,
,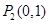 ,
,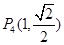 .
.
于是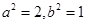 .
.
所以 椭圆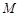 的方程为:
的方程为: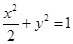 . 2分
. 2分
(Ⅱ)①当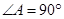 时,设直线
时,设直线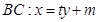 ,由
,由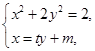 得
得 .设
.设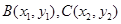 ,则
,则 ,
,
所以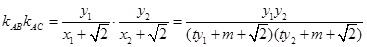
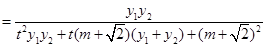
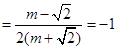 .
.
于是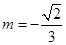 ,此时
,此时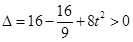 ,所以 直线
,所以 直线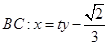 .
.
因为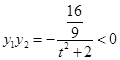 ,故线段
,故线段 与
与 轴相交于
轴相交于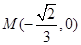 ,即原点在线段
,即原点在线段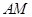 的延长线上,即原点在
的延长线上,即原点在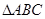 的外部,符合题设. 6分
的外部,符合题设. 6分
所以 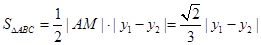
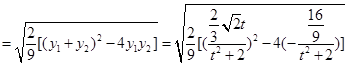
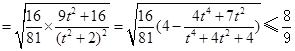 .
.
当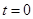 时取到最大值
时取到最大值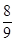 . 9分
. 9分
②当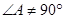 时,不妨设
时,不妨设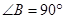

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
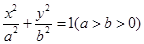 的右焦点为F2(1,0),点
的右焦点为F2(1,0),点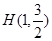 在椭圆上.
在椭圆上.
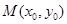 在圆
在圆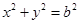 上,M在第一象限,过M作圆
上,M在第一象限,过M作圆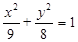 的焦点为焦点,且过
的焦点为焦点,且过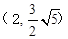 点的双曲线的标准方程.
点的双曲线的标准方程.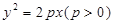 ,其准线方程为
,其准线方程为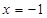 ,过准线与
,过准线与 轴的交点
轴的交点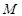 做直线
做直线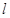 交抛物线于
交抛物线于 两点.
两点.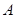 为
为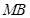 中点,求直线
中点,求直线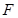 ,当
,当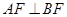 时,求
时,求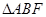 的面积.
的面积. :
: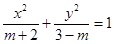
 .
.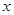 轴上的椭圆,求
轴上的椭圆,求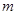 的取值范围;
的取值范围;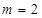 ,过点
,过点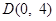 的直线
的直线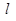 与曲线
与曲线 ,
,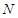 两点,
两点, 为坐标原点,若
为坐标原点,若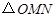 为直角三角形,求直线
为直角三角形,求直线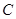 :
: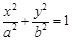 (
(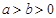 )过点
)过点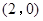 ,且椭圆
,且椭圆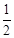 .
.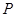 在直线
在直线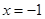 上,过
上,过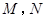 两点,且
两点,且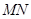 中点,再过
中点,再过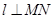 .证明:直线
.证明:直线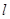 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.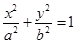
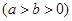 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为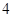 ,且过点
,且过点 .
. 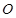 为坐标原点,斜率为
为坐标原点,斜率为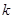 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点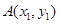 ,
,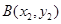 ,若
,若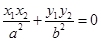 ,求△
,求△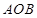 的面积.
的面积.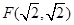 及直线
及直线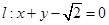 ,曲线
,曲线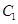 是满足下列两个条件的动点
是满足下列两个条件的动点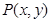 的轨迹:①
的轨迹:①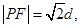 其中
其中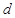 是
是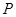 到直线
到直线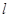 的距离;②
的距离;②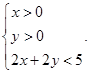
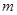 与曲线
与曲线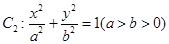 均相切于同一点,求椭圆
均相切于同一点,求椭圆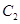 离心率
离心率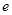 的取值范围.
的取值范围. 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长为
轴上,长轴长为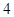 ,且点
,且点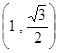 在椭圆
在椭圆 是椭圆
是椭圆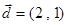 的直线
的直线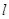 交椭圆
交椭圆 、
、 两点,求证:
两点,求证: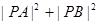 为定值.
为定值.