题目内容
已知sin（
+α）=
，则cos（
-α）= ．
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
考点：运用诱导公式化简求值,两角和与差的余弦函数
专题：三角函数的求值
分析：直接利用诱导公式化简求值即可．
解答：
解：sin（
+α）=cos（
-
-α）=cos（
-α）=
，
∴cos（
-α）=
．
故答案为：
．
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 3 |
∴cos（
| π |
| 4 |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查诱导公式的应用，三角函数打火机求值，基本知识的考查．
练习册系列答案
相关题目
定义在实数集R上的函数y=f（x）的图象是连续不断的，若对任意的实数x，存在不为0的常数r使得f（x+r）=-rf（x）恒成立，则称f（x）是一个“关于r函数”，下列“关于r函数”的结论正确的是（ ）
| A、f（x）=0是常数函数中唯一一个“关于r函数” | ||
| B、f（x）=x2是一个“关于r函数” | ||
| C、f（x）=sinπx不是一个“关于r函数” | ||
D、“关于
|
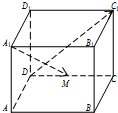如图所示，在棱长为1的正方体ABCD-A1B1C1D1中，M是棱CD的中点，则| A1M |
| DC1 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
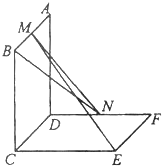如图，已知两个正方形ABCD 和DCEF不在同一平面内，且平面ABCD⊥平面DCEF，M，N分别为AB，DF的中点．