题目内容
已知f1(x)=sinx+cosx，记f2(x)=f′1(x)，f3(x)=f′2=(x)，…，fn(x)=f′n-1=(x)，(n∈N*，n≥2)，则f1(
)+f2(
)+…+f2007(
)=__________.
答案：-1 【解析】本题考查了导数的概念及周期数列的求和、三角函数的周期性问题.
由已知可得f2(x)=cosx-sinx,f3(x)=-sinx-cosx,f4(x)=-cosx+sinx,f5(x)=sinx+cosx,
f6(x)=f2(x),f7(x)=f3(x),…,即得fn(x)为以4为周期的数列.∵fl(x)+f2(x)+f3(x)+f4(x)=0,
∴f1()+f2()+f3()+…+f2007(
)=f2005(
)+f2006,(
)+f2007(
)
=f1(
)+f2(
)+f3(
)=f4(
)=cos
-sin
=-1.
练习册系列答案
相关题目
)+f2(
)+…+f2 007(
)=_____________.
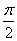)＋f2(
)+f2(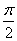
)+…+f2 012(
)=（ ）。
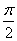) + f2(