题目内容
已知函数 .
.
(1)求证不论 为何实数,
为何实数, 总是增函数;
总是增函数;
(2)确定 的值,使
的值,使 为奇函数;
为奇函数;
(3)当 为奇函数时,求
为奇函数时,求 的值域.
的值域.
 .
.(1)求证不论
 为何实数,
为何实数, 总是增函数;
总是增函数;(2)确定
 的值,使
的值,使 为奇函数;
为奇函数;(3)当
 为奇函数时,求
为奇函数时,求 的值域.
的值域.(Ⅰ)见下(Ⅱ) (Ⅲ)
(Ⅲ)
 (Ⅲ)
(Ⅲ)
试题分析:(1)函数的单调性的证明有两种基本的方法.一是定义法;而是利用导数.在目前阶段,我们只能用定义来证明函数的单调性.即分三个步骤:①设值②作差③比较差值与0的关系.(2)作为奇函数,满足
 ,可求得
,可求得 的值.(Ⅲ)求函数的值域,根据函数解析式的特点,有各种不同的方法,一般有直接观察法、换元法、单调性法、判别式法、图像法等.本题中函数值域的求得较为简单,用直接观察法即可.
的值.(Ⅲ)求函数的值域,根据函数解析式的特点,有各种不同的方法,一般有直接观察法、换元法、单调性法、判别式法、图像法等.本题中函数值域的求得较为简单,用直接观察法即可.试题解析(1)∵
 的定义域为R,任取
的定义域为R,任取
则

∵
 ∴
∴ ,
,
∴
 即
即
∴不论
 为何实数
为何实数 总为增函数, 6分
总为增函数, 6分(2)∵
 为奇函数,∴
为奇函数,∴
即
 解得
解得 8分
8分(3)由(2)

∵
 ∴
∴ ∴
∴
∴

∴
 的值域为
的值域为 12分
12分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 ,
, .
. 的图象与
的图象与 轴无交点,求
轴无交点,求 的取值范围;
的取值范围; 上存在零点,求
上存在零点,求 ,
, .当
.当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使得
,使得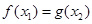 ,求
,求 的取值范围.
的取值范围. ,
, ,其中实数
,其中实数 .
.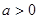 ,求函数
,求函数 的单调区间;
的单调区间; 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.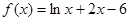 的零点所在的区间为( )
的零点所在的区间为( ) 对任意实数
对任意实数 均成立,则实数
均成立,则实数 的取值范围是( )
的取值范围是( )



 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b] D,使得函数
D,使得函数 ; ②、
; ②、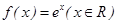 ;
; ; ④、
; ④、 .
.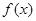 的定义域为D,若对于任意
的定义域为D,若对于任意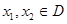 ,当
,当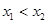 时都有
时都有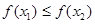 ,则称函数
,则称函数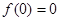 ;②
;②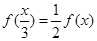 ;③
;③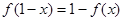 ,则
,则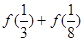 等于( )
等于( )


 ,求
,求 =
=