题目内容
 如图所示,已知边长为2的正方形ABCD所在平面外有一点P,PA⊥平面ABCD,且PA=2,E是PC的中点.
如图所示,已知边长为2的正方形ABCD所在平面外有一点P,PA⊥平面ABCD,且PA=2,E是PC的中点.(1)证明:平面BDE⊥平面PAC;
(2)求:BE与平面ABCD所成角的余弦值.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知条件推导出AC⊥BD,BD⊥PA,由经能证明平面BDE⊥平面PAC.
(2)连结OE,由已知条件推导出∠EBO是BE与平面ABCD所成角,由此能求出BE与平面ABCD所成角的余弦值.
(2)连结OE,由已知条件推导出∠EBO是BE与平面ABCD所成角,由此能求出BE与平面ABCD所成角的余弦值.
解答:
(1)证明:∵正方形ABCD,∴AC⊥BD,
∵PA⊥平面ABCD,BD?平面ABCD,
∴BD⊥PA,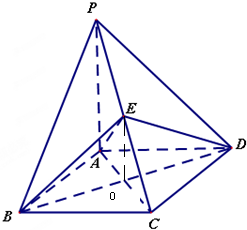
∵PA∩AC=A,∴BD⊥平面PAC,
∵BD?平面BDE,∴平面BDE⊥平面PAC.
(2)解:连结OE,∵ABCD是边长为2的正方形,
∴O是AC中点,又E是PC的中点,
∴OE∥PA,且OE=
PA=1,
∵PA⊥平面ABCD,∴OE⊥平面ABCD,
∴∠EBO是BE与平面ABCD所成角,
∵BO=
=
,∴BE=
=
,
∴cos∠EBO=
=
.
∴BE与平面ABCD所成角的余弦值为
.
∵PA⊥平面ABCD,BD?平面ABCD,
∴BD⊥PA,

∵PA∩AC=A,∴BD⊥平面PAC,
∵BD?平面BDE,∴平面BDE⊥平面PAC.
(2)解:连结OE,∵ABCD是边长为2的正方形,
∴O是AC中点,又E是PC的中点,
∴OE∥PA,且OE=
| 1 |
| 2 |
∵PA⊥平面ABCD,∴OE⊥平面ABCD,
∴∠EBO是BE与平面ABCD所成角,
∵BO=
| 1 |
| 2 |
| 4+4 |
| 2 |
| 2+1 |
| 3 |
∴cos∠EBO=
| ||
|
| ||
| 3 |
∴BE与平面ABCD所成角的余弦值为
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查直线与平面所成有的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取12名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取12名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶): 如图为150辆汽车通过某路段时速度的频率分布直方图.根据提供的频率分布直方图,求下列问题:
如图为150辆汽车通过某路段时速度的频率分布直方图.根据提供的频率分布直方图,求下列问题: