题目内容
1．已知$\left\{\begin{array}{l}2x-y≤0\\ x-3y+5≥0\\ y≥1\end{array}\right.$，则x+y-2的最小值是（ ）| A． | 12 | B． | -3 | C． | 6 | D． | 4 |
分析 作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z=x+y对应的直线进行平移，可得当x=-2，y=1时，z=x+y取得最小值为-1，从而求出x+y-1的值．
解答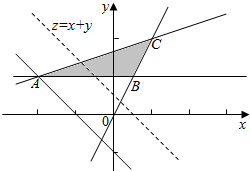 
解：作出不等式组表示的平面区域，
得到如图的△ABC及其内部，其中A（-2，1），B（$\frac{1}{2}$，1），C（1，2）
设z=F（x，y）=x+y，将直线l：z=x+y进行平移，
当l经过点A（-2，1）时，目标函数z达到最小值
∴z最小值=F（-2，1）=-1，
故x+y-2=z-2=-1-2=-3，
故选：B．
点评 本题给出二元一次不等式组，求目标函数z=x+y的最小值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
12．函数$f（x）=\left\{{\begin{array}{l}{x+1（x≤-1）}\\{{x^2}（-1＜x＜2）}\\{2x（x≥2）}\end{array}}\right.$，若f（x）=2，则x的值是（ ）
| A． | $\sqrt{2}$ | B． | $±\sqrt{2}$ | C． | 0或1 | D． | $\sqrt{3}$ |
9．已知$\frac{{\sqrt{2}}}{2}（sin\frac{α}{2}-cos\frac{α}{2}）=\frac{1}{3}$，则sinα的值为（ ）
| A． | $-\frac{{\sqrt{3}}}{3}$ | B． | $-\frac{1}{3}$ | C． | $\frac{2}{9}$ | D． | $\frac{7}{9}$ |