题目内容
己知等差数列{an},公差d>0,前n项和为Sn,且满足a2a3=45,a1+a4=14.
(I)求数列{an}的通项公式及前,n项和Sn;
(II)设bn=
,若数列{bn}也是等差数列,试确定非零常数c;并求数列{
}的前n项和Tn.
(I)求数列{an}的通项公式及前,n项和Sn;
(II)设bn=
| Sn |
| n+c |
| 1 |
| bn•bn+1 |
(Ⅰ)由等差数列{an}的性质可得a2+a3=a1+a4=14,又a2a3=45.
∴
,解得
或
,
∵d>0,∴
应舍去,
因此
.
∴d=a3-a2=4,a1=a2-d=5-4=1,
∴an=1+(n-1)×4=4n-3,
Sn=n+
×4=2n2-n.
(Ⅱ)由(Ⅰ)可得bn=
,
∵数列{bn}是等差数列,则2b2=b1+b3,即2×
=
+
.
解得c=-
.
∴bn=2n.
=
=
(
-
).
∴Tn=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)
=
.
∴
|
|
|
∵d>0,∴
|
因此
|
∴d=a3-a2=4,a1=a2-d=5-4=1,
∴an=1+(n-1)×4=4n-3,
Sn=n+
| n(n-1) |
| 2 |
(Ⅱ)由(Ⅰ)可得bn=
| 2n2-n |
| n+c |
∵数列{bn}是等差数列,则2b2=b1+b3,即2×
| 6 |
| 2+c |
| 1 |
| 1+c |
| 15 |
| 3+c |
解得c=-
| 1 |
| 2 |
∴bn=2n.
| 1 |
| bnbn+1 |
| 1 |
| 2n•2(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 4 |
| 1 |
| n+1 |
=
| n |
| 4(n+1) |

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
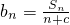 ,若数列{bn}也是等差数列,试确定非零常数c;并求数列
,若数列{bn}也是等差数列,试确定非零常数c;并求数列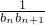 的前n项和Tn.
的前n项和Tn. ,若数列{bn}也是等差数列,试确定非零常数c;并求数列
,若数列{bn}也是等差数列,试确定非零常数c;并求数列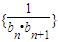 的前n项和Tn.
的前n项和Tn.