题目内容
已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于点A(0,1)对称.
的图象关于点A(0,1)对称.
(I)求![]() 的值;
的值;
(II)若![]() ,且
,且![]() 在区间
在区间![]() 上为减函数,求实数
上为减函数,求实数![]() 的取值范围;
的取值范围;
(III)在条件(II)下,试证明函数![]() 与函数
与函数![]() 图象的交点不可能落在
图象的交点不可能落在![]() 轴的左侧.
轴的左侧.
(I)![]()
(II)![]() .
.
(III)证明见解析
解析:
(I)设P(![]() )为函数
)为函数![]() 图象上任意一点,点P关于点A的对称点为Q(
图象上任意一点,点P关于点A的对称点为Q(![]() ),则有
),则有
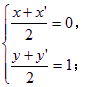 即
即![]() .………………………………………………2分
.………………………………………………2分
![]() 点Q在
点Q在![]() 上,
上,![]() ,
,
![]() ,即
,即![]() ,
,![]() .………………… 4分
.………………… 4分
(II)![]() 。设任意
。设任意![]()
![]() ,且
,且![]() ,
,
则![]() ,……………………… 7分
,……………………… 7分
对一切![]() 恒成立.
恒成立.
![]() 对一切
对一切![]() 恒成立,
恒成立,
![]() . ………………………………………………… 9分
. ………………………………………………… 9分
(III)![]() .……………………………… 10分
.……………………………… 10分
(证法一)假设两曲线的交点在![]() 轴左侧,即交点的横坐标
轴左侧,即交点的横坐标![]() .…11分
.…11分
则![]() 且
且![]() ,
,![]() ,即
,即![]() .
.
这与假设![]() 矛盾,故两曲线的交点不可能在
矛盾,故两曲线的交点不可能在![]() 轴左侧.………………… 14分
轴左侧.………………… 14分
(证法二)假设两曲线的交点在![]() 轴的左侧,即交点的横坐标
轴的左侧,即交点的横坐标![]() .
.
![]() 若
若![]() ,则
,则![]() ,而
,而![]() ,与假设矛盾;
,与假设矛盾;
![]() 若
若![]() ,则
,则![]() ,而
,而![]() ,与假设矛盾.
,与假设矛盾.
故曲线![]() 与曲线
与曲线![]() 的交点不可能在
的交点不可能在![]() 轴左侧.……………………… 14分
轴左侧.……………………… 14分
(若用其它方法,可依据该标准合理赋分)

练习册系列答案
相关题目
 的图象与函数
的图象与函数 的图象恰有两个交点,则实数k的取值范围是_________.
的图象恰有两个交点,则实数k的取值范围是_________. 的图象与
的图象与 轴分别相交于点
轴分别相交于点 ,
,  (
(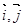 分别是与
分别是与 .
.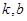 的值;
的值; 满足
满足 时,求函数
时,求函数 的最小值.
的最小值.