Question

(本小题满分12分)已知函数的图象与轴分别相交于点,

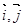（分别是与轴正半轴同方向的单位向量）,函数.

（1）求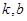的值;

（2）当满足时,求函数的最小值.

 

Answer 1

【答案】

（1）k=1,b=2.（2）-3.

【解析】

试题分析：(1)由已知得A(,0),B(0,b),则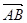=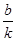（,b）,于是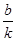="2,b=2." ∴k=1,b=2.

(2)由f(x)> g(x),得x+2>x²-x-6,即(x+2)(x-4)<0, 得-2<x<4,

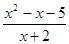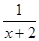==x+2+-5

由于x+2>0,则≥-3,其中等号当且仅当x+2=1,即x=-1时成立

∴的最小值是-3.

考点：向量的坐标；一次函数、二次函数的性质；基本不等式。

点评：（1）向量的坐标就是其终点的坐标减去起点的坐标。(2)注意基本不等式应用的条件：一正二定三相等。本题把式子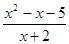化为x+2+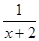-5的形式，从而达到利用基本不等式的条件。