题目内容

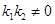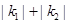已知M、N是椭圆上关于原点对称的两点，P是椭圆上任意一点，且直线PM、PN的斜率分别为k1、k2（），若的最小值为1，则椭圆的离心率为            。

 

【答案】

【解析】解：设P（acosβ，bsinβ），M（acosα，bsinα），则N（-acosα，-bsinα），

可得k1=b(sinβ-sinα) a(cosβ-cosα) ，k2=b(sinβ+sinα) a(cosβ+cosα) ，

|k1|•|k2|=|b2(sin2β-sin2α) a2(cos2β-cos2α) |=b2 a2 ，

∴|k1|+|k2|≥2 |k1k2| =2b a ⇒2b a =1⇒e= 3  2 ．

 

练习册系列答案
相关题目
已知C：
x2
a2
+
y2
b2
=1(a＞b＞0)椭圆具有性质：若M，N是椭圆上关于原点O对称的两点，点P是椭圆上任意一点，当直线PM，PN的斜率都存在，并记为kPM，kPN时，那么kPM与kPN之积是与点P的位置无关的定值，试写出双曲线
x2
a2
-
y2
b2
=1具有类似特性的性质并加以证明．
已知A、B是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)长轴的两个端点，M，N是椭圆上关于x轴对称的两点，直线AM，BN的斜率分别为k1，k2，且k1k2≠0．若|k1|+|k2|的最小值为1，则椭圆的离心率（　　）
A、
1
2
B、
2
2
C、
3
2
D、
2
3
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)，M，N是椭圆上关于原点对称的两点，P是椭圆上任意一点，且直线PM、PN的斜率分别为k1、k2，若|k1k2|=
1
4
，则椭圆的离心率为（　　）
已知椭圆方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，A、B分别是椭圆长轴的两个端点，M，N是椭圆上关于x轴对称的两点，直线AM，BN的斜率分别为k1，k2，若|k1•k2|=
1
4
，则椭圆的离心率为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网