题目内容
已知数列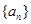 为
为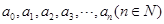 ,
,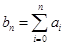 表示
表示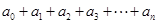 ,
,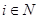 .
.
⑴若数列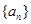 为等比数列
为等比数列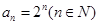 ,求
,求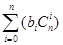 ;
;
⑵若数列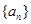 为等差数列
为等差数列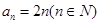 ,求
,求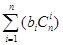 .
.
(1) , (2)
, (2) .
.
解析试题分析:(1)注意到 ,只需求出
,只需求出 代入相应位置,整理即可得到其值,但要注意二项式定理及二项式系数和的应用;(2)此小题中
代入相应位置,整理即可得到其值,但要注意二项式定理及二项式系数和的应用;(2)此小题中 ,则
,则 ,以下采用构造关系式,应用导数法与赋值法求得其值.
,以下采用构造关系式,应用导数法与赋值法求得其值.
试题解析:⑴ ,所以
,所以


 ;
;
⑵ ,
, ,
,
因为 ,
,
两边同乘以 ,则有
,则有 ,
,
两边求导,左边 ,
,
右边 ,
,
即 (*),
(*),
对(*)式两边再求导,得
取 ,则有
,则有
所以 .
.
考点:二项式定理,求导公式,赋值法,转化思想.

练习册系列答案
相关题目
 (n为正偶数)的展开式中第5项的二项式系数最大,则第5项是 .
(n为正偶数)的展开式中第5项的二项式系数最大,则第5项是 .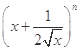 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.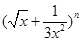 的第五项的二项式系数与第三项的二项式系数的比是
的第五项的二项式系数与第三项的二项式系数的比是 ,
, 的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-
的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-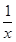 )2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
)2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项. 展开式中不含
展开式中不含 项的系数的和为 .
项的系数的和为 .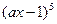 的展开式中
的展开式中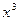 的系数是80,则实数
的系数是80,则实数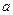 的值是 .
的值是 . 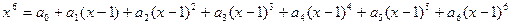 ,则
,则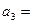 。
。