题目内容
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2
,且到直线l:y=x-2的距离为
,满足条件的点P的个数为
| 2 |
| 2 |
1
1
(个).分析:先求出双曲线的方程,并画出图形,因为直线与双曲线的渐近线平行,所以只能有一个点满足要求.
解答: 解:∵|PM|-|PN|=2
解:∵|PM|-|PN|=2
<4=|MN|,
∴据双曲线的定义可知:动点P应在双曲线上,
-
=1,其中,a=
,c=2,
∴b2=22-(
)2=2.
∴动点P的轨迹为x2-y2=2.
如图所示:∵双曲线为等轴双曲线,∴其渐近线方程为y=±x,
而直线y=x与y=x-2的距离d=
=
,
∴直线y=x-2的左上方的双曲线上的点都不满足到直线y=x-2上的距离等于
.
在双曲线上的点到直线y=x-2的距离为
的点只能在直线y=x-2的下方,且只有一个点,如图示.
故答案为1.
 解:∵|PM|-|PN|=2
解:∵|PM|-|PN|=2| 2 |
∴据双曲线的定义可知:动点P应在双曲线上,
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
∴b2=22-(
| 2 |
∴动点P的轨迹为x2-y2=2.
如图所示:∵双曲线为等轴双曲线,∴其渐近线方程为y=±x,
而直线y=x与y=x-2的距离d=
| |-2-0| | ||
|
| 2 |
∴直线y=x-2的左上方的双曲线上的点都不满足到直线y=x-2上的距离等于
| 2 |
在双曲线上的点到直线y=x-2的距离为
| 2 |
故答案为1.
点评:理解与等轴双曲线的渐近线平行的直线只能与双曲线有一个交点是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
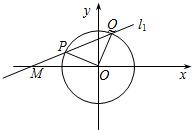 已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的
已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的