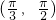题目内容
若锐角α使得sinα=tanα-cosα成立,则α的范围是( )A.

B.

C.

D.

【答案】分析:由题意可得sinα+cosα=tanα,即  sin(α+
sin(α+ )=tanα,由正弦函数的定义域和值域求得1<tanα≤
)=tanα,由正弦函数的定义域和值域求得1<tanα≤ ,由此可得锐角α的范围.
,由此可得锐角α的范围.
解答:解:∵锐角α使得sinα=tanα-cosα成立,
∴sinα+cosα=tanα,
∴ sin(α+
sin(α+ )=tanα,由
)=tanα,由  <α<
<α< ,可得
,可得  <α+
<α+ <
< ,
,
 ≥
≥ sin(α+
sin(α+ )≥
)≥ ×
× ,
,
∴1<tanα≤ ,
,
故α的范围是 ,
,
故选C.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于中档题.
 sin(α+
sin(α+ )=tanα,由正弦函数的定义域和值域求得1<tanα≤
)=tanα,由正弦函数的定义域和值域求得1<tanα≤ ,由此可得锐角α的范围.
,由此可得锐角α的范围.解答:解:∵锐角α使得sinα=tanα-cosα成立,
∴sinα+cosα=tanα,
∴
 sin(α+
sin(α+ )=tanα,由
)=tanα,由  <α<
<α< ,可得
,可得  <α+
<α+ <
< ,
, ≥
≥ sin(α+
sin(α+ )≥
)≥ ×
× ,
,∴1<tanα≤
 ,
,故α的范围是
 ,
,故选C.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目