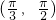题目内容
若锐角α使得sinα=tanα-cosα成立,则α的范围是( )
分析:由题意可得sinα+cosα=tanα,即
sin(α+
)=tanα,由正弦函数的定义域和值域求得1<tanα≤
,由此可得锐角α的范围.
| 2 |
| π |
| 4 |
| 2 |
解答:解:∵锐角α使得sinα=tanα-cosα成立,
∴sinα+cosα=tanα,
∴
sin(α+
)=tanα,由
<α<
,可得
<α+
<
,
≥
sin(α+
)≥
×
,
∴1<tanα≤
,
故α的范围是(
,
),
故选C.
∴sinα+cosα=tanα,
∴
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
∴1<tanα≤
| 2 |
故α的范围是(
| π |
| 4 |
| π |
| 3 |
故选C.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目