题目内容
试求圆C:x2+y2-x+2y=0关于直线l:x-y+1=0对称的曲线C′的方程.
活动:学生先思考,然后解答,教师引导学生抓住本质的东西,即圆的圆心坐标变化、半径不变,另外可利用相关点法来求.
解法一:设P′(x,y)为所求曲线C′上任意一点,P′关于l的对称点为P(x0,y0),则P(x0,y0)在圆C上.由题意可得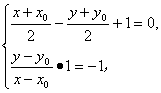 解得
解得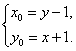 (*)
(*)
因为P(x0,y0)在圆C上,所以x02+y02-x0+2y0=0.
将(*)代入得(y-1)2+(x+1)2-(y-1)+2(x+1)=0,
化简得x2+y2+4x-3y+5=0,即为C′的方程.
解法二:(特殊对称)圆C关于直线l的对称图形仍然是圆,且半径不变,故只需求圆心C′,即求(![]() ,-1)关于直线l:x-y+1=0的对称点C′(-2,
,-1)关于直线l:x-y+1=0的对称点C′(-2,![]() ),因此所求圆C′的方程为(x+2)2+(y
),因此所求圆C′的方程为(x+2)2+(y![]() )2=
)2=![]() .
.
点评:比较解法一与解法二看出,利用几何性质解题往往较简单.

练习册系列答案
相关题目
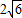 ,求圆C的方程.
,求圆C的方程. ,求圆C的方程.
,求圆C的方程.