题目内容
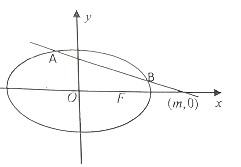
【题目】已知动点
到两定点
，
距离之和为4（
），且动点的轨迹曲线
过点
.
（1）求
的值；
（2）若直线
与曲线有不同的两个交点
，且
（
为坐标原点），求
的值.
【答案】（1）
；（2）
【解析】
（1）由椭圆的定义可知，点M的轨迹C是以两定点
，
为焦点，长半轴长为2的椭圆，由此可设曲线C的方程，代入点
求得b；
（2）将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程，再结合根与系数的关系利用向量的数量积坐标公式即可求得k的值．
（1）依题意
，即4>2m知：曲线C是以两定点
，
为焦点，长半轴长为2的椭圆，所以
，
设曲线
的方程为
，代入点
解得
，由
解得
所以
（2）由（1）知曲线的方程为
，设点
，
，
联立方程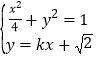
，消去
得
，
，得 
，
，
则
=
得
，
所以
的值 .
【题目】某媒体为调查喜爱娱乐节目
是否与观众性别有关，随机抽取了30名男性和30名女性观众，抽查结果用等高条形图表示如图：
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 |
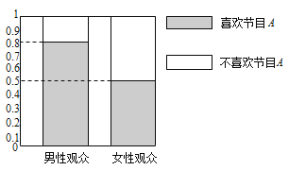
（1）根据该等高条形图，完成右上
列联表，并用独立性检验的方法分析，则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目与观众性别有关？
（2）从男性观众中按喜欢节目与否，用分层抽样的方法抽取5名做进一步调查．从这5名中任选2名，求恰有1名喜欢节目和1名不喜欢节目的概率．
附：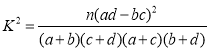
| 0.100 | 0.050 | 0.010 | 0.00 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】随着移动支付的普及，中国人的生活方式正悄然巨变，带智能手机，不带钱包出门还渐成为中国人的新习惯
年我国移动支付增长迅猛，据统计，某支付平台2017年移动支付的笔数占总支付笔数的
．
Ⅰ
从该支付平台2017年的所有支付中任取10笔，求移动支付笔数的期望和方差；
Ⅱ现有500名使用该支付平台的用户，其中300名是城市用户，200名是农村用户，调查他们2017年个人移动支付的比例是否达到了，得到
列联表如下：
个人移动支付达到了 | 个人移动支付达到了 | 合计 | |
城市用户 | 270 | 30 | 300 |
农村用户 | 170 | 30 | 200 |
合计 | 440 | 60 | 500 |
根据上表数据，问是否有
的把握认为2017年个人移动支付比例达到了与该用户是城市用户还是农村用户有关？
附：
|
|
|
k |
|
|
